
【题目】如图,在三棱台ABCDEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.

(1)求证:BF⊥平面ACFD;
(2)求二面角B-AD-F的平面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)由面面垂直性质定理得AC⊥平面BCFE,因此BF⊥AC.再根据平几知识得BF⊥FC.最后根据线面垂直判定定理得结论(2)过点F作FQ⊥AK于Q,由三垂线定理得BQ⊥AK.即∠BQF是二面角B-AD-F的平面角.再根据解三角形得二面角B-AD-F的平面角的余弦值
试题解析:(1)证明 延长AD,BE,CF相交于一点K,如图所示.
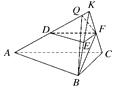
因为平面BCFE⊥平面ABC,平面BCFE∩平面ABC=BC,且AC⊥BC,
所以AC⊥平面BCFE,因此BF⊥AC.
又因为EF∥BC,BE=EF=FC=1,BC=2,所以△BCK为等边三角形,且F为CK的中点,则BF⊥CK,且CK∩AC=C,CK,AC都在平面ACFD内,
所以BF⊥平面ACFD.
(2)过点F作FQ⊥AK于Q,连接BQ.
因为BF⊥平面ACFD,AK在平面ACFD内,所以BF⊥AK,
则AK⊥平面BQF,BQ在平面BQF内,所以BQ⊥AK.
所以∠BQF是二面角B-AD-F的平面角.
在Rt△ACK中,AC=3,CK=2,得FQ=![]() .
.
在Rt△BQF中,FQ=![]() ,BF=
,BF=![]() ,得cos∠BQF=
,得cos∠BQF=![]() .
.
所以,二面角B-AD-F的平面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出
.现从参与关注生态文明建设的人群中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第
人按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)求出这![]() 人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(Ⅲ)现在要从年龄较小的第![]() 、
、![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,则第
人,则第![]() 、
、![]() 组分别抽取多少人?
组分别抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线C的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,其一个顶点的坐标是(0,1).
,其一个顶点的坐标是(0,1).
(Ⅰ)求双曲线C的标准方程;
(Ⅱ)若直线![]() 与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线
与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线![]() 的方程
的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的图像可由
的图像可由![]() 的图像平移得到,对于任意的实数
的图像平移得到,对于任意的实数![]() ,均有
,均有![]() 成立,且存在实数
成立,且存在实数![]() ,使得
,使得![]() 为奇函数.
为奇函数.
(Ⅰ)求函数![]() 的解析式.
的解析式.
(Ⅱ)函数![]() 的图像与直线
的图像与直线![]() 有两个不同的交点
有两个不同的交点![]() ,
, ![]() ,若
,若![]() ,
,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a,E、F、G、H分别为AB、BC、CD、DA的中点.若沿EF、FG、GH、HE将四角折起,试问能折成一个四棱锥吗?为什么?你从中能得到什么结论?对于圆锥有什么类似的结论?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 上顶点为
上顶点为![]() ,右焦点为
,右焦点为![]() ,过右顶点
,过右顶点![]() 作直线
作直线![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,又在直线
,又在直线![]() 和椭圆
和椭圆![]() 上分别取点
上分别取点![]() 和点
和点![]() ,满足
,满足![]() (
(![]() 为坐标原点),连接
为坐标原点),连接![]() .
.

(1)求![]() 的值,并证明直线
的值,并证明直线![]() 与圆
与圆![]() 相切;
相切;
(2)判断直线![]() 与圆
与圆![]() 是否相切?若相切,请证明;若不相切,请说明理由.
是否相切?若相切,请证明;若不相切,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=![]() ,则下列结论中错误的是
,则下列结论中错误的是

A.AC⊥BE B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值 D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:(1)异面直线是指空间两条既不平行也不相交的直线;(2)若直线![]() 上有两点到平面
上有两点到平面![]() 的距离相等,则
的距离相等,则![]() ;(3)若直线
;(3)若直线![]() 与平面
与平面![]() 内无穷多条直线都垂直,则
内无穷多条直线都垂直,则![]() ;(4)两条异面直线中的一条垂直于平面
;(4)两条异面直线中的一条垂直于平面![]() ,则另一条必定不垂直于平面
,则另一条必定不垂直于平面![]() .其中正确命题的个数是 ( )
.其中正确命题的个数是 ( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com