
【题目】设![]() .求最大的整数
.求最大的整数![]() ,使得集合S有k个互不相同的非空子集,具有性质:对这k个子集中任意两个不同子集,若它们的交非空,则它们交集中的最小元素与这两个子集中的最大元素均不相同.
,使得集合S有k个互不相同的非空子集,具有性质:对这k个子集中任意两个不同子集,若它们的交非空,则它们交集中的最小元素与这两个子集中的最大元素均不相同.
【答案】![]()
【解析】
对有限非空实数集A,用![]() 与
与![]() 分别表示集合A的最小元素与最大元素.
分别表示集合A的最小元素与最大元素.
考虑集合S的所有包含1且至少有两个元素的子集.
注意到,![]() ,
,
故![]() .
.
于是,这样的子集一共![]() 个.
个.
显然满足要求.
接下来证明:当![]() 时,不存在满足要求的k个子集.
时,不存在满足要求的k个子集.
用数学归纳法证明:对整数![]() ,在集合
,在集合![]() 的任意
的任意![]() 个不同非空子集
个不同非空子集![]() 中,存在两个子集
中,存在两个子集![]() ,满足
,满足![]() ,且
,且![]() . ①
. ①
显然,只需对![]() 的情形证明上述结论.
的情形证明上述结论.
当![]() 时,将
时,将![]() 的全部七个非空子集分成三组,
的全部七个非空子集分成三组,
第一组:{3},{1,3},{2,3};
第二组:{2},{1,2};
第三组:{1},{1,2,3}.
由抽屉原理,知任意四个非空子集必有两个在同一组中, 取同组中的两个子集分别记为![]() ,在排在前面的记为
,在排在前面的记为![]() ,则满足结论①.
,则满足结论①.
假设结论在![]() 时成立.考虑
时成立.考虑![]() 时的情形.
时的情形.
若![]() 中至少有
中至少有![]() 个子集不含
个子集不含![]() ,对其中的
,对其中的![]() 个子集用归纳假设,知存在两个子集满足结论①.
个子集用归纳假设,知存在两个子集满足结论①.
若至多有![]() -1个子集不含
-1个子集不含![]() ,则至少有
,则至少有![]() +1个子集含
+1个子集含![]() ,将其中
,将其中![]() +1个子集均去掉
+1个子集均去掉![]() ,得到{1,2,…,n}的
,得到{1,2,…,n}的![]() +1个子集.
+1个子集.
由于{1,2,…,n}的全体子集可分为![]() 组,每组两个子集互补,故由抽屉原理,知在上述
组,每组两个子集互补,故由抽屉原理,知在上述![]() +1个子集中一定有两个属于同一组,即互为补集.
+1个子集中一定有两个属于同一组,即互为补集.
因此,相应地有两个子集![]() 满足
满足![]() ,这两个集合显然满足结论①.
,这两个集合显然满足结论①.
于是,![]() 时结论成立.
时结论成立.
综上,![]() .
.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
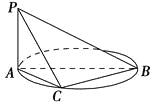
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则方程
,则方程![]() 无实根”的否命题;
无实根”的否命题;
②命题“在![]() 中,
中,![]() ,那么
,那么![]() 为等边三角形”的逆命题;
为等边三角形”的逆命题;
③命题“若![]() ,则
,则![]() ”的逆否命题;
”的逆否命题;
④“若![]() ,则
,则![]() 的解集为
的解集为![]() ”的逆命题;
”的逆命题;
其中真命题的序号为( )
A.①②③④B.①②④C.②④D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点![]() ,
,![]() 两点,且圆心C在直线
两点,且圆心C在直线![]() 上.
上.
(1)求圆C的方程;
(2)设![]() ,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使
,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使![]() 是常数,若存在,求出点N坐标;若不存在,说明理由.
是常数,若存在,求出点N坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电信公司为了加强新用5G技术的推广使用,为该公司的用户制定了一套5G月消费返流量费的套餐服务方案;当月消费金额不超过100元时,按消费金额的![]() 进行返还;当月消费金额超过100元时,除消费金额中的100元仍按
进行返还;当月消费金额超过100元时,除消费金额中的100元仍按![]() 进行返还外,若另超出100元的部分消费金额为A元,则超过部分按
进行返还外,若另超出100元的部分消费金额为A元,则超过部分按![]() 进行返还,记用户当月返还所得流量费y(单位:元),消费金额x(单位:元)
进行返还,记用户当月返还所得流量费y(单位:元),消费金额x(单位:元)
(1)写出该公司用户月返还所得流量费的函数模型;
(2)如果用户小李当月获返还的流量费是12元,那么他这个月的消费金额是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科技改变生活,方便生活.共享单车的使用就是云服务的一种实践,它是指企业与政府合作,为居民出行提供单车共享服务,它符合低碳出行理念,为解决城市出行的“最后一公里”提供了有力支撑,是共享经济的一种新形态.某校学生社团为研究当地使用共享单车人群的年龄状况,随机抽取了当地![]() 名使用共享单车的群众作出调查,所得频率分布直方图如图所示.
名使用共享单车的群众作出调查,所得频率分布直方图如图所示.
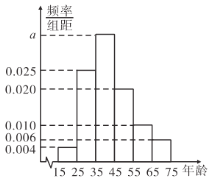
(1)估计当地共享单车使用者年龄的中位数;
(2)若按照分层抽样从年龄在![]() ,
,![]() 的人群中抽取
的人群中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人调查单车使用体验情况,记抽取的
人调查单车使用体验情况,记抽取的![]() 人中年龄在
人中年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘.如下图所示,从左到右有ABC三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有一个原则:一次只能移动一个盘子且大盘子不能在小盘子上面,则移动的次数为_______(用![]() 表示)
表示)
A B
B C
C
查看答案和解析>>
科目:高中数学 来源: 题型:
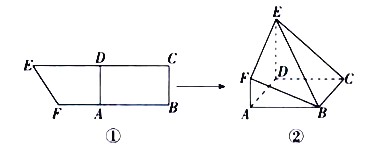
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,且
,且![]() (①).将四边形
(①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() (②).在折起的过程中,下列说法中正确的是( )
(②).在折起的过程中,下列说法中正确的是( )
A.![]() 平面
平面![]()
B.![]() 四点不可能共面
四点不可能共面
C.若![]() ,则平面
,则平面![]() 平面
平面![]()
D.平面![]() 与平面
与平面![]() 可能垂直
可能垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com