
ЁОЬтФПЁПФГбЇаЃЮЊСЫСЫНтИУаЃбЇЩњЖдгкФГЯюдЫЖЏЕФАЎКУЪЧЗёгыадБ№гаЙиЃЌЭЈЙ§ЫцЛњГщВщ110УћбЇЩњЃЌЕУЕНШчЯТ2ЁС2ЕФСаСЊБэЃК
ЯВЛЖИУЯюдЫЖЏ | ВЛЯВЛЖИУЯюдЫЖЏ | змМЦ | |
Фа | 40 | 20 | 60 |
ХЎ | 20 | 30 | 50 |
змМЦ | 60 | 50 | 110 |
гЩЙЋЪНK2= ![]() ЃЌЫуЕУK2Ёж7.61
ЃЌЫуЕУK2Ёж7.61
ИНБэЃК
pЃЈK2Ёнk0ЃЉ | 0.025 | 0.01 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
ВЮееИНБэЃЌвдЯТНсТле§ШЗЪЧЃЈ ЃЉ
A.га99.5%вдЩЯЕФАбЮеШЯЮЊЁААЎКУИУЯюдЫЖЏгыадБ№гаЙиЁБ
B.га99.5%вдЩЯЕФАбЮеШЯЮЊЁААЎКУИУЯюдЫЖЏгыадБ№ЮоЙиЁБ
C.га99%вдЩЯЕФАбЮеШЯЮЊЁААЎКУИУЯюдЫЖЏгыадБ№гаЙиЁБ
D.га99%вдЩЯЕФАбЮеШЯЮЊЁААЎКУИУЯюдЫЖЏгыадБ№ЮоЙиЁБ

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=lnЃЈ2ax+1ЃЉ+ ![]() Љx2Љ2axЃЈaЁЪRЃЉЃЎ
Љx2Љ2axЃЈaЁЪRЃЉЃЎ
ЃЈ1ЃЉШєx=2ЮЊfЃЈxЃЉЕФМЋжЕЕуЃЌЧѓЪЕЪ§aЕФжЕЃЛ
ЃЈ2ЃЉШєy=fЃЈxЃЉдк[3ЃЌ+ЁоЃЉЩЯЮЊдіКЏЪ§ЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБa=Љ ![]() ЪБЃЌЗНГЬfЃЈ1ЉxЃЉ=
ЪБЃЌЗНГЬfЃЈ1ЉxЃЉ= ![]() гаЪЕИљЃЌЧѓЪЕЪ§bЕФзюДѓжЕЃЎ
гаЪЕИљЃЌЧѓЪЕЪ§bЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЕїВщжааЁбЇПЮЭтЪЙгУЛЅСЊЭјЕФЧщПіЃЌНЬг§ВПЯђЛЊЖЋЁЂЛЊББЁЂЛЊФЯКЭЮїВПЕиЧј60ЫљжааЁбЇЗЂГіЮЪОэ![]() ЗнЃЌ
ЗнЃЌ ![]() УћбЇЩњВЮМгСЫЮЪОэЕїВщЃЌВЂИљОнЫљЕУЪ§ОнЛГібљБОЕФЦЕТЪЗжВМжБЗНЭМЃЈШчЭМЃЉ.
УћбЇЩњВЮМгСЫЮЪОэЕїВщЃЌВЂИљОнЫљЕУЪ§ОнЛГібљБОЕФЦЕТЪЗжВМжБЗНЭМЃЈШчЭМЃЉ.
ЃЈ1ЃЉвЊДгет![]() УћжааЁбЇжагУЗжВуГщбљЕФЗНЗЈГщШЁ
УћжааЁбЇжагУЗжВуГщбљЕФЗНЗЈГщШЁ![]() УћжааЁбЇЩњНјвЛВНЕїВщЃЌдђдк
УћжааЁбЇЩњНјвЛВНЕїВщЃЌдђдк![]() ЃЈаЁЪБЃЉЪБМфЖЮФкгІГщГіЕФШЫЪ§ЪЧЖрЩйЃП
ЃЈаЁЪБЃЉЪБМфЖЮФкгІГщГіЕФШЫЪ§ЪЧЖрЩйЃП
ЃЈ2ЃЉШєЯЃЭћ![]() ЕФжааЁбЇЩњУПЬьЪЙгУЛЅСЊЭјЪБМфВЛЩйгк
ЕФжааЁбЇЩњУПЬьЪЙгУЛЅСЊЭјЪБМфВЛЩйгк![]() ЃЈаЁЪБЃЉЃЌЧыЙРМЦ
ЃЈаЁЪБЃЉЃЌЧыЙРМЦ![]() ЕФжЕЃЌВЂЫЕУїРэгЩ.
ЕФжЕЃЌВЂЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгЂИёРМзуЧђГЌМЖСЊШќ,МђГЦгЂГЌ,ЪЧгЂЙњзуЧђзюИпЕШМЖЕФжАвЕзуЧђСЊШќ,вВЪЧЪРНчзюИпЫЎЦНЕФжАвЕзуЧђСЊШќжЎвЛ,ФПЧАгЂГЌВЮШќЧђЖгга20Иі,дк2014-2015ШќМОНсЪјКѓНЋИїЖгЛ§ЗжЗжГЩ6ЖЮ,ВЂЛцжЦГіСЫШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМ(ЭМжаИїЗжзщЧјМфАќРЈзѓЖЫЕу,ВЛАќРЈгвЖЫЕу,ШчЕквЛзщБэЪОЛ§Зждк[30,40)Фк).ИљОнЭМжаЯжгааХЯЂ,НтД№ЯТУцЮЪЬт:

(Ђё)ЧѓЛ§Зждк[40,50)ФкЕФЦЕТЪ,ВЂВЙШЋетИіЦЕТЪЗжВМжБЗНЭМ;
(Ђђ)ДгЛ§Зждк[40,60)жаЕФЧђЖгжаШЮбЁШЁ2ИіЧђЖг,ЧѓбЁШЁЕФ2ИіЧђЖгЕФЛ§ЗждкЦЕТЪЗжВМжБЗНЭМжаДІгкВЛЭЌзщЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌBC=aЃЌAC=bЃЌЧвaЃЌbЪЧЗНГЬ![]() ЕФСНИљЃЌ2cos(A+B)=1ЃЎ
ЕФСНИљЃЌ2cos(A+B)=1ЃЎ
(1)ЧѓЁЯCЕФЖШЪ§ЃЛ
(2)ЧѓABЕФГЄЃЛ
(3)ЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЮЊЦцКЏЪ§ЃЌЕБxЁн0ЪБЃЌfЃЈxЃЉ= ![]() ЃЎgЃЈxЃЉ=
ЃЎgЃЈxЃЉ= ![]() ЃЌ
ЃЌ
ЃЈ1ЃЉЧѓЕБxЃМ0ЪБЃЌКЏЪ§fЃЈxЃЉЕФНтЮіЪНЃЌВЂдкИјЖЈжБНЧзјБъЯЕФкЛГіfЃЈxЃЉдкЧјМф[Љ5ЃЌ5]ЩЯЕФЭМЯѓЃЛЃЈВЛгУСаБэУшЕуЃЉ 
ЃЈ2ЃЉИљОнвбжЊЬѕМўжБНгаДГіgЃЈxЃЉЕФНтЮіЪНЃЌВЂЫЕУїgЃЈxЃЉЕФЦцХМадЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЫФУцЬхABCDЕФЖЅЕуЖМдкЧђOБэУцЩЯЃЌЧвAB=BC=AC=2 ![]() ЃЌDA=DB=DC=2ЃЌЙ§ADзїЯрЛЅДЙжБЕФЦНУцІСЁЂІТЃЌШєЦНУцІСЁЂІТНиЧђOЫљЕУНиУцЗжБ№ЮЊдВMЁЂNЃЌдђЃЈ ЃЉ
ЃЌDA=DB=DC=2ЃЌЙ§ADзїЯрЛЅДЙжБЕФЦНУцІСЁЂІТЃЌШєЦНУцІСЁЂІТНиЧђOЫљЕУНиУцЗжБ№ЮЊдВMЁЂNЃЌдђЃЈ ЃЉ
A.MNЕФГЄЖШЪЧЖЈжЕ ![]()
B.MNГЄЖШЕФзюаЁжЕЪЧ2
C.дВMУцЛ§ЕФзюаЁжЕЪЧ2Іа
D.дВMЁЂNЕФУцЛ§КЭЪЧЖЈжЕ8Іа
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉТњзуfЃЈxЃЉ=fЃЈ ![]() ЃЉЃЌЕБxЁЪ[1ЃЌ4]ЪБЃЌfЃЈxЃЉ=lnxЃЌШєдкЧјМфxЁЪ[
ЃЉЃЌЕБxЁЪ[1ЃЌ4]ЪБЃЌfЃЈxЃЉ=lnxЃЌШєдкЧјМфxЁЪ[ ![]() ЃЌ4]ФкЃЌКЏЪ§gЃЈxЃЉ=fЃЈxЃЉЉaxгыxжсгаШ§ИіВЛЭЌЕФНЛЕуЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ЃЌ4]ФкЃЌКЏЪ§gЃЈxЃЉ=fЃЈxЃЉЉaxгыxжсгаШ§ИіВЛЭЌЕФНЛЕуЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛЏМђ
ЃЈ1ЃЉ![]()
ЃЈ2ЃЉ![]()
ЁОД№АИЁП(1) ![]() ЃЛ(2)
ЃЛ(2) ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЧаЛЏЯвПЩЕУШ§НЧКЏЪ§ЪНЕФжЕЮЊЃ1
ЃЈ2ЃЉНсКЯШ§НЧКЏЪ§ЕФаджЪПЩЕУШ§НЧКЏЪ§ЪНЕФжЕЮЊ![]()
ЪдЬтНтЮіЃК
ЃЈ1ЃЉtan70Ёуcos10ЁуЃЈ ![]() tan20ЁуЉ1ЃЉ
tan20ЁуЉ1ЃЉ
=cot20Ёуcos10ЁуЃЈ ![]() Љ1ЃЉ
Љ1ЃЉ
=cot20Ёуcos10ЁуЃЈ![]() ЃЉ
ЃЉ
=![]() ЁСcos10ЁуЁСЃЈ
ЁСcos10ЁуЁСЃЈ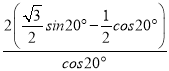 ЃЉ
ЃЉ
=![]() ЁСcos10ЁуЁСЃЈ
ЁСcos10ЁуЁСЃЈ![]() ЃЉ
ЃЉ
=![]() ЁСЃЈЉ
ЁСЃЈЉ![]() ЃЉ
ЃЉ
=Љ1
ЃЈ2ЃЉЁпЃЈ1+tan1ЁуЃЉЃЈ1+tan44ЁуЃЉ=1+ЃЈtan1Ёу+tan44ЁуЃЉ+tan1Ёуtan44Ёу
=1+tanЃЈ1Ёу+44ЁуЃЉ[1Љtan1Ёуtan44Ёу]+tan1Ёуtan44Ёу=2ЃЎ
ЭЌРэПЩЕУЃЈ1+tan2ЁуЃЉЃЈ1+tan43ЁуЃЉ
=ЃЈ1+tan3ЁуЃЉЃЈ1+tan42ЁуЃЉ
=ЃЈ1+tan4ЁуЃЉЃЈ1+tan41ЁуЃЉ=Ё=2ЃЌ
ЙЪ![]() =
=![]()
ЕуОІЃКШ§НЧКЏЪ§ЪНЕФЛЏМђвЊзёбЁАШ§ПДЁБддђ:вЛПДНЧЃЌетЪЧживЊвЛЛЗЃЌЭЈЙ§ПДНЧжЎМфЕФВюБ№гыСЊЯЕЃЌАбНЧНјааКЯРэЕФВ№ЗжЃЌДгЖје§ШЗЪЙгУЙЋЪН ЃЛЖўПДКЏЪ§УћГЦЃЌПДКЏЪ§УћГЦжЎМфЕФВювьЃЌДгЖјШЗЖЈЪЙгУЕФЙЋЪНЃЌГЃМћЕФгаЧаЛЏЯвЃЛШ§ПДНсЙЙЬиеїЃЌЗжЮіНсЙЙЬиеїЃЌПЩвдАяжњЮвУЧевЕНБфаЮЕФЗНЯђЃЌШчгіЕНЗжЪНвЊЭЈЗжЕШ.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
18
ЁОЬтФПЁПЦНУцФкИјЖЈШ§ИіЯђСП![]()
ЃЈ1ЃЉЧѓ![]()
ЃЈ2ЃЉЧѓТњзу![]() ЕФЪЕЪ§
ЕФЪЕЪ§![]() .
.
ЃЈ3ЃЉШє![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() .
.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com