
ΓΨΧβΡΩΓΩ”ΔΗώάΦΉψ«ρ≥§ΦΕΝΣ»ϋ,Φρ≥Τ”Δ≥§, «”ΔΙζΉψ«ρΉνΗΏΒ»ΦΕΒΡ÷Α“ΒΉψ«ρΝΣ»ϋ,“≤ « άΫγΉνΗΏΥ°ΤΫΒΡ÷Α“ΒΉψ«ρΝΣ»ϋ÷°“Μ,ΡΩ«Α”Δ≥§≤Έ»ϋ«ρΕ””–20Ηω,‘Ύ2014-2015»ϋΦΨΫα χΚσΫΪΗςΕ”ΜΐΖ÷Ζ÷≥…6ΕΈ,≤ΔΜφ÷Τ≥ωΝΥ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ(ΆΦ÷–ΗςΖ÷Ήι«χΦδΑϋά®ΉσΕΥΒψ,≤ΜΑϋά®”“ΕΥΒψ,»γΒΎ“ΜΉι±μ ΨΜΐΖ÷‘Ύ[30,40)ΡΎ).ΗυΨίΆΦ÷–œ÷”––≈œΔ,Ϋβ¥πœ¬ΟφΈ Χβ:

(Δώ)«σΜΐΖ÷‘Ύ[40,50)ΡΎΒΡΤΒ¬ ,≤Δ≤Ι»Ϊ’βΗωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ;
(Δρ)¥”ΜΐΖ÷‘Ύ[40,60)÷–ΒΡ«ρΕ”÷–»Έ―Γ»Γ2Ηω«ρΕ”,«σ―Γ»ΓΒΡ2Ηω«ρΕ”ΒΡΜΐΖ÷‘ΎΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–¥Π”Ύ≤ΜΆ§ΉιΒΡΗ≈¬ .
ΓΨ¥πΑΗΓΩ(1)ΦϊΫβΈω;(2) P=![]() .
.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΗ≈¬ ΚΆΈΣ1ΒΟΒΫΗ≈¬ ÷Β;(2)Ι≈ΒδΗ≈–ΆΘ§ΦΤΥψ≥ω ¬ΦΰΉή ΐΈΣ21ΦΰΘ§¬ζΉψΧθΦΰΒΡ ¬Φΰ ΐΈΜ7ΦΰΘ§ΫχΕχΒΟΒΫΗ≈¬ ÷Β.
ΫβΈωΘΚ
(I)ΜΐΖ÷‘Ύ[40,50)ΡΎΒΡΤΒ¬ ΈΣ
1-(0.030+0.010+0.015+0.015+0.005)ΓΝ10=0.25,![]() =0.025,
=0.025,
Ι ≤Ι»ΪΒΡΆΦ–Έ»γΆΦΥυ Ψ

(Δρ)ΜΐΖ÷‘Ύ[40,50)ΡΎΒΡ«ρΕ””–20ΓΝ0.025ΓΝ10=5Ηω,Ζ÷±πΦ«ΈΣA,B,C,D,E,ΜΐΖ÷‘Ύ[50,60)ΡΎΒΡ«ρΕ””–20x0.010ΓΝ10=2Ηω,Ζ÷±πΦ«ΈΣm,n,
Υυ“‘,‘Ύ7Ηω«ρΕ”÷–―Γ»Γ2Ηω,Μυ±Ψ ¬Φΰ”–(A,B),(A,C),(A,D),(A,E),(A,m),(A,n),(B,C),(B,D),(B,E),(B,m),(B,n),(C,D),(C,E),(C,m),(C,n),(D,E),(D,m),(D,n),(E,m),(E,n),(m,n)Ι≤21Ηω,
Τδ÷–ΖϊΚœ―Γ»ΓΒΡΝΫΗω«ρΕ”ΒΡΜΐΖ÷‘ΎΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–¥Π”Ύ≤ΜΆ§ΉιΒΡΜυ±Ψ ¬Φΰ”–10Ηω,Ι ―Γ»ΓΒΡΝΫΗω«ρΕ”ΜΐΖ÷‘ΎΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–¥Π”Ύ≤ΜΆ§ΉιΒΡΗ≈¬ ΈΣP=![]() .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚΚ· ΐ![]()
![]() «σΚ· ΐ
«σΚ· ΐ![]() ΒΡ÷ήΤΎT”κΒΞΒς‘ω«χΦδΘ°
ΒΡ÷ήΤΎT”κΒΞΒς‘ω«χΦδΘ°
![]() Κ· ΐ
Κ· ΐ![]() ”κ
”κ![]() ΒΡΆΦœσ”–ΦΗΗωΙΪΙ≤ΫΜΒψΘ°
ΒΡΆΦœσ”–ΦΗΗωΙΪΙ≤ΫΜΒψΘ°
![]() …ηΙΊ”ΎxΒΡΚ· ΐ
…ηΙΊ”ΎxΒΡΚ· ΐ![]() ΒΡΉν–Γ÷ΒΈΣ
ΒΡΉν–Γ÷ΒΈΣ![]() Θ§ ‘»ΖΕ®¬ζΉψ
Θ§ ‘»ΖΕ®¬ζΉψ![]() ΒΡaΒΡ÷ΒΘ°
ΒΡaΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–ΓΆθΓΔ–Γ’≈ΝΫΈΜΆ§―ßΆφΆΕ÷ά’ΐΥΡΟφΧεΘ®ΟΩΗωΟφΕΦΈΣΒ»±Ώ»ΐΫ«–ΈΒΡ’ΐ»ΐάβΉΕΘ©ςΜΉ”Θ®ςΜΉ”÷ ΒΊΨυ‘»Θ§ΗςΟφ…œΒΡΒψ ΐΖ÷±πΈΣ![]() Θ©”ΈœΖΘ§Ιφ‘ρΘΚ–ΓΆθœ÷÷ά“ΜΟΕςΜΉ”Θ§œρœ¬ΒΡΒψ ΐΦ«ΈΣ
Θ©”ΈœΖΘ§Ιφ‘ρΘΚ–ΓΆθœ÷÷ά“ΜΟΕςΜΉ”Θ§œρœ¬ΒΡΒψ ΐΦ«ΈΣ![]() Θ§–Γ’≈Κσ÷ά“ΜΟΕςΜΉ”Θ§œρœ¬ΒΡΒψ ΐΦ«ΈΣ
Θ§–Γ’≈Κσ÷ά“ΜΟΕςΜΉ”Θ§œρœ¬ΒΡΒψ ΐΦ«ΈΣ![]() Θ§
Θ§
Θ®1Θ©‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§“‘
÷–Θ§“‘![]() ΈΣΉχ±ξΒΡΒψΙ≤”–ΦΗΗωΘΩ ‘«σΒψ
ΈΣΉχ±ξΒΡΒψΙ≤”–ΦΗΗωΘΩ ‘«σΒψ![]() ¬δ‘Ύ÷±œΏ
¬δ‘Ύ÷±œΏ![]() …œΒΡΗ≈¬ ΘΜ
…œΒΡΗ≈¬ ΘΜ
Θ®2Θ©ΙφΕ®ΘΚ»τ![]() Θ§‘ρ–ΓΆθ”°Θ§»τ
Θ§‘ρ–ΓΆθ”°Θ§»τ![]() Θ§‘ρ–Γ’≈”°Θ§ΤδΥϊ«ιΩω≤ΜΖ÷ δ”°Θ§ ‘Έ ’βΗω”ΈœΖΙΪΤΫ¬πΘΩ«κΥΒΟςάμ”….
Θ§‘ρ–Γ’≈”°Θ§ΤδΥϊ«ιΩω≤ΜΖ÷ δ”°Θ§ ‘Έ ’βΗω”ΈœΖΙΪΤΫ¬πΘΩ«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ,“―÷ΣA,B,CΈΣ÷±Ϋ«Ήχ±ξœΒxOy÷–ΒΡ»ΐΗωΕ®Βψ
(Δώ)»τΒψDΈΣΓθABCDΒΡΒΎΥΡΗωΕΞΒψ,«σ|![]() |;
|;
(Δρ)»τΒψP‘Ύ÷±œΏOC…œ,«“![]() ΓΛ
ΓΛ![]() =4,«σΒψPΒΡΉχ±ξ.
=4,«σΒψPΒΡΉχ±ξ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐfΘ®xΘ©= ![]() Θ§gΘ®xΘ©=aΘ®x+bΘ©Θ®0ΘΦaΓή1Θ§bΓή0Θ©Θ°
Θ§gΘ®xΘ©=aΘ®x+bΘ©Θ®0ΘΦaΓή1Θ§bΓή0Θ©Θ°
Θ®1Θ©Χ÷¬έΚ· ΐy=fΘ®xΘ©gΘ®xΘ©ΒΡΤφ≈Φ–‘ΘΜ
Θ®2Θ©Β±b=0 ±Θ§≈–ΕœΚ· ΐy= ![]() ‘ΎΘ®©¹1Θ§1Θ©…œΒΡΒΞΒς–‘Θ§≤ΔΥΒΟςάμ”…ΘΜ
‘ΎΘ®©¹1Θ§1Θ©…œΒΡΒΞΒς–‘Θ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©…ηhΘ®xΘ©=|af2Θ®xΘ©©¹ ![]() |Θ§»τhΘ®xΘ©ΒΡΉν¥σ÷ΒΈΣ2Θ§«σa+bΒΡ»Γ÷ΒΖΕΈßΘ°
|Θ§»τhΘ®xΘ©ΒΡΉν¥σ÷ΒΈΣ2Θ§«σa+bΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηy=f(t) «Ρ≥ΗέΩΎΥ°ΒΡ…νΕ»y(ΟΉ)ΙΊ”Ύ ±Φδt(–Γ ±)ΒΡΚ· ΐΘ§Τδ÷–![]() .œ¬±μ «ΗΟΗέΩΎΡ≥“ΜΧλ¥”0 ±÷Ν24 ±Φ«¬ΦΒΡ ±Φδt”κΥ°…νyΒΡΙΊœΒΘΚ
.œ¬±μ «ΗΟΗέΩΎΡ≥“ΜΧλ¥”0 ±÷Ν24 ±Φ«¬ΦΒΡ ±Φδt”κΥ°…νyΒΡΙΊœΒΘΚ
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 12 | 15.1 | 12.1 | 9.1 | 12 | 14.9 | 11.9 | 9 | 12.1 |
Ψ≠≥ΛΤΎΙέ≤λΘ§Κ· ΐy=f(t)ΒΡΆΦœσΩ…“‘ΫϋΥΤΒΊΩ¥≥…Κ· ΐ![]() ΒΡΆΦœσ.Δ≈«σ
ΒΡΆΦœσ.Δ≈«σ![]() ΒΡΫβΈω ΫΘΜΔΤ…ηΥ°…ν≤Μ–Γ”Ύ
ΒΡΫβΈω ΫΘΜΔΤ…ηΥ°…ν≤Μ–Γ”Ύ![]() ΟΉ ±Θ§¬÷¥§≤≈ΡήΫχ≥ωΗέΩΎΓΘΡ≥¬÷¥§‘Ύ“Μ÷γ“ΙΡΎ“ΣΫχΗέΩΎΩΩΑΕΑλ ¬Θ§»ΜΚσ‘Ό≥ωΗέΓΘΈ ΗΟ¬÷¥§ΉνΕύΡή‘ΎΗέΩΎΆΘΩΩΕύ≥Λ ±ΦδΘΩ
ΟΉ ±Θ§¬÷¥§≤≈ΡήΫχ≥ωΗέΩΎΓΘΡ≥¬÷¥§‘Ύ“Μ÷γ“ΙΡΎ“ΣΫχΗέΩΎΩΩΑΕΑλ ¬Θ§»ΜΚσ‘Ό≥ωΗέΓΘΈ ΗΟ¬÷¥§ΉνΕύΡή‘ΎΗέΩΎΆΘΩΩΕύ≥Λ ±ΦδΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥―ß–ΘΈΣΝΥΝΥΫβΗΟ–Θ―ß…ζΕ‘”ΎΡ≥œν‘ΥΕ·ΒΡΑ°ΚΟ «Ζώ”κ–‘±π”–ΙΊΘ§Ά®ΙΐΥφΜζ≥ι≤ι110Οϊ―ß…ζΘ§ΒΟΒΫ»γœ¬2ΓΝ2ΒΡΝ–ΝΣ±μΘΚ
œ≤ΜΕΗΟœν‘ΥΕ· | ≤Μœ≤ΜΕΗΟœν‘ΥΕ· | ΉήΦΤ | |
Ρ– | 40 | 20 | 60 |
š | 20 | 30 | 50 |
ΉήΦΤ | 60 | 50 | 110 |
”…ΙΪ ΫK2= ![]() Θ§ΥψΒΟK2Γ÷7.61
Θ§ΥψΒΟK2Γ÷7.61
ΗΫ±μΘΚ
pΘ®K2Γίk0Θ© | 0.025 | 0.01 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
≤Έ’’ΗΫ±μΘ§“‘œ¬Ϋα¬έ’ΐ»Ζ «Θ® Θ©
A.”–99.5%“‘…œΒΡΑ―Έ’»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±π”–ΙΊΓ±
B.”–99.5%“‘…œΒΡΑ―Έ’»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±πΈόΙΊΓ±
C.”–99%“‘…œΒΡΑ―Έ’»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±π”–ΙΊΓ±
D.”–99%“‘…œΒΡΑ―Έ’»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±πΈόΙΊΓ±
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–{an}ΒΡ«ΑnœνΚΆΈΣSn Θ§ «“Ε‘»Έ“β’ΐ’ϊ ΐnΘ§ΕΦ”–3an=2Sn+3≥…ΝΔΘ°
Θ®1Θ©«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©…ηbn=log3an Θ§ «σ ΐΝ–{ ![]() }ΒΡ«ΑnœνΚΆTn Θ°
}ΒΡ«ΑnœνΚΆTn Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±»ΐάβ÷υABC©¹A1B1C1÷–Θ§ΓœABC=90ΓψΘ§EΓΔFΖ÷±πΈΣA1C1ΓΔB1C1ΒΡ÷–ΒψΘ§DΈΣάβCC1…œ»Έ“ΜΒψΘ°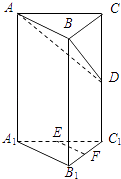
Θ®ΔώΘ©«σ÷ΛΘΚ÷±œΏEFΓΈΤΫΟφABDΘΜ
Θ®ΔρΘ©«σ÷ΛΘΚΤΫΟφABDΓΆΤΫΟφBCC1B1 Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com