
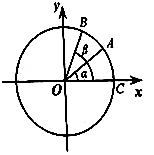
 如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$).
如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$).分析 (Ⅰ)先求出向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的坐标,再跟它们的夹角的余弦值cos∠AOB=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}|•|\overrightarrow{OB}|}$,计算求得结果.
(Ⅱ)设∠AOB的平分线OD交单位圆于点D,则∠COD=$\frac{α+β}{2}$,求得$\overrightarrow{OD}$的坐标,根据$\overrightarrow{OD}•\overrightarrow{AB}$=0,求得tan$\frac{α+β}{2}$的值.
解答 解:(Ⅰ)在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点
A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$),
∴$\overrightarrow{OA}$=($\frac{4}{5}$,$\frac{3}{5}$),$\overrightarrow{OB}$=($\frac{5}{13}$,$\frac{12}{13}$),|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,
∴$\overrightarrow{OA}$,$\overrightarrow{OB}$夹角的余弦值cos∠AOB=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}|•|\overrightarrow{OB}|}$=$\frac{\frac{20}{65}+\frac{36}{65}}{1•1}$=$\frac{56}{65}$.
(Ⅱ)设∠AOB的平分线OD交单位圆于点D,则∠COD=$\frac{α+β}{2}$,
从而D(cos$\frac{α+β}{2}$,sin$\frac{α+β}{2}$),∴$\overrightarrow{OD}$=(cos$\frac{α+β}{2}$,sin$\frac{α+β}{2}$),
连接AB,可知OD⊥AB,即$\overrightarrow{OD}•\overrightarrow{AB}$=0.
∴$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$=(-$\frac{27}{65}$,$\frac{21}{65}$),
∴(cos$\frac{α+β}{2}$,sin$\frac{α+β}{2}$)•(-$\frac{27}{65}$,$\frac{21}{65}$)=-$\frac{27}{65}$•cos$\frac{α+β}{2}$+$\frac{21}{65}$•sin$\frac{α+β}{2}$=0,
∴tan$\frac{α+β}{2}$=$\frac{9}{7}$.
点评 本题考查综合运用平面向量与三角函数解决问题的能力,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a?α,b?β,α∥β | B. | a∥α,b?β | C. | a⊥α,b⊥α | D. | a⊥α,b?α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{y}^{2}}{3}$-x2=1 | D. | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com