Question

3．圆台的侧面积为$\frac{16}{3}$πcm²，它的内切球的表面积是4πcm²，则圆台的体积为$\frac{26}{9}$πcm³．

Answer 1

分析 设圆台的上底面半径为r，下底面半径为R，由切线长定理得母线长为R+r，
由圆台的侧面面积和内切球表面积求出r和R，高是圆台内切球的直径a，由此求出圆台的体积．

解答 解：设圆台的上底面半径为r，下底面半径为R，则母线长为R+r；
设圆台内切球的半径为a，则4πa²=4π，解得a=1；
又圆台的侧面面积是π•（r+R）²=$\frac{16}{3}$π，
解得r+R=$\frac{4}{3}$$\sqrt{3}$①；
画出圆台的轴截面，如图所示：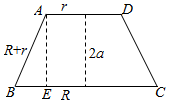

则R-r=$\sqrt{{（R+r）}^{2}{-（2a）}^{2}}$=$\sqrt{\frac{16}{3}-4}$=$\frac{2}{3}$$\sqrt{3}$②，
由①②解得R=$\sqrt{3}$，r=$\frac{1}{3}$$\sqrt{3}$；
∴圆台的体积为V=$\frac{1}{3}$π（r²+rR+R²）h=$\frac{1}{3}$π（$\frac{1}{3}$+$\frac{1}{3}$$\sqrt{3}$×$\sqrt{3}$+3）×2=$\frac{26}{9}$π（cm³）．
故答案为：$\frac{26}{9}$π．

点评 本题考查了圆台的结构特征与面积、体积的计算问题，根据线切长定理得出母线长为R+r，是简化解题的关键．