
已知等差数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
(1)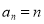 ;(2)
;(2)
【解析】
试题分析:(1)等差数列基本量的求解是等差数列的一类基本问题,解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用;(2)等比数列基本量的求解是等比数列的一类基本问题,解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用,尤其需要注意的是,在使用等比数列的前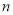 项和公式时,应该要分类讨论,有时还应善于运用整体代换的思想简化运算过程;(3)解题时要善于类比要能正确区分等差、等比的性质,不要把两者的性质搞混了.
项和公式时,应该要分类讨论,有时还应善于运用整体代换的思想简化运算过程;(3)解题时要善于类比要能正确区分等差、等比的性质,不要把两者的性质搞混了.
试题解析:(1)由题意得
 公差
公差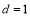
所以通项公式为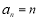
(2)数列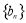 是公比为2,首项为2的等比数列,
是公比为2,首项为2的等比数列,
所以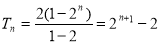
考点:1、等差数列的通项公式;2、等比数列的前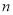 项和.
项和.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源:2015届福建省等三校高三上学期期中联考理科数学试卷(解析版) 题型:解答题
(本题满分14分) 己知函数 (其中
(其中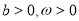 )的最大值为
)的最大值为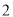 ,直线
,直线 是
是 图象的任意两条对称轴,且
图象的任意两条对称轴,且 的最小值为
的最小值为 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)若 ,求
,求 的值;
的值;
(3)对 ,在区间
,在区间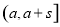 上
上 有且只有
有且只有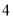 个零点,请直接写出满足条件的所有
个零点,请直接写出满足条件的所有 的值并把上述结论推广到一般情况.(不要求证明)
的值并把上述结论推广到一般情况.(不要求证明)
查看答案和解析>>
科目:高中数学 来源:2015届福建省、德化一中高三9月摸底考试文科数学试卷(解析版) 题型:解答题
已知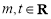 ,函数
,函数 .
.
(1)当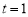 时,若
时,若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若关于 的不等式
的不等式 在区间
在区间 上有解,求
上有解,求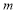 的取值范围;
的取值范围;
(3)已知曲线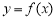 在其图象上的两点
在其图象上的两点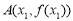 ,
,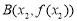 (
(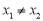 )处的切线分别为
)处的切线分别为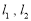 .若直线
.若直线 与
与 平行,试探究点
平行,试探究点 与点
与点 的关系,并证明你的结论.
的关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2015届福建省、德化一中高三9月摸底考试文科数学试卷(解析版) 题型:选择题
设 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,若对任意的
上的两个函数,若对任意的 ,都有
,都有 ,则称
,则称 和
和 在
在 上是“密切函数”,
上是“密切函数”, 称为“密切区间”,设
称为“密切区间”,设 与
与 在
在 上是“密切函数”,则它的“密切区间”可以是( )
上是“密切函数”,则它的“密切区间”可以是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届福建省八县(市高三上学期半期联考理科数学试卷(解析版) 题型:选择题
偶函数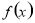 满足
满足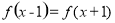 ,且在
,且在 时,
时,  ,
,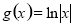 ,
,
则函数 与
与 图象交点的个数是( )
图象交点的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com