
【题目】设a,b,c,d均为正数,且a+b=c+d,证明:
(1)若ab>cd,则 ![]() +
+ ![]() >
> ![]() +
+ ![]() ;
;
(2)![]() +
+ ![]() >
> ![]() +
+ ![]() 是|a﹣b|<|c﹣d|的充要条件.
是|a﹣b|<|c﹣d|的充要条件.
【答案】
(1)证明:由于( ![]() +
+ ![]() )2=a+b+2
)2=a+b+2 ![]() ,
,
( ![]() +
+ ![]() )2=c+d+2
)2=c+d+2 ![]() ,
,
由a,b,c,d均为正数,且a+b=c+d,ab>cd,
则 ![]() >
> ![]() ,
,
即有( ![]() +
+ ![]() )2>(
)2>( ![]() +
+ ![]() )2,
)2,
则 ![]() +
+ ![]() >
> ![]() +
+ ![]()
(2)证明:①若 ![]() +
+ ![]() >
> ![]() +
+ ![]() ,则(
,则( ![]() +
+ ![]() )2>(
)2>( ![]() +
+ ![]() )2,
)2,
即为a+b+2 ![]() >c+d+2
>c+d+2 ![]() ,
,
由a+b=c+d,则ab>cd,
于是(a﹣b)2=(a+b)2﹣4ab,
(c﹣d)2=(c+d)2﹣4cd,
即有(a﹣b)2<(c﹣d)2,即为|a﹣b|<|c﹣d|;
②若|a﹣b|<|c﹣d|,则(a﹣b)2<(c﹣d)2,
即有(a+b)2﹣4ab<(c+d)2﹣4cd,
由a+b=c+d,则ab>cd,
则有( ![]() +
+ ![]() )2>(
)2>( ![]() +
+ ![]() )2.
)2.
综上可得, ![]() +
+ ![]() >
> ![]() +
+ ![]() 是|a﹣b|<|c﹣d|的充要条件
是|a﹣b|<|c﹣d|的充要条件
【解析】(1)运用不等式的性质,结合条件a,b,c,d均为正数,且a+b=c+d,ab>cd,即可得证;(2)从两方面证,①若 ![]() +
+ ![]() >
> ![]() +
+ ![]() ,证得|a﹣b|<|c﹣d|,②若|a﹣b|<|c﹣d|,证得
,证得|a﹣b|<|c﹣d|,②若|a﹣b|<|c﹣d|,证得 ![]() +
+ ![]() >
> ![]() +
+ ![]() ,注意运用不等式的性质,即可得证.
,注意运用不等式的性质,即可得证.
【考点精析】本题主要考查了不等式的证明的相关知识点,需要掌握不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
| |||||
|
|
| |||
|
(1)请结合所给表格,在所给的坐标系中作出函数![]() 一个周期内的简图;
一个周期内的简图;

(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求![]() 的最大值和最小值及相应
的最大值和最小值及相应![]() 的取值.
的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2-4ax+1+b(a>0)的定义域为[2,3],值域为[1,4];设g(x)=![]() .
.
(1)求a,b的值;
(2)若不等式g(2x)-k2x≥0在x∈[1,2]上恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )
)
(1)若![]() ,用“五点法”在给定的坐标系中,画出函数
,用“五点法”在给定的坐标系中,画出函数![]() 在[0,π]上的图象.
在[0,π]上的图象.

(2)若![]() 偶函数,求
偶函数,求![]()
(3)在(2)的前提下,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 在
在![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为改善职工的出行条件,随机抽取50名职工,调查他们的居住地与公司的距离d(单位:千米).若样本数据分组为[0,2],(2,4],(4,6],(6,8],(8,10],(10,12],由数据绘制的分布频率直方图如图所示,则样本中职工居住地与公司的距离不超过4千米的人数为人. 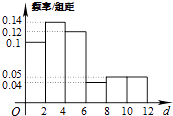
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2bx+a(a,b∈R)
(1)若a从集合{0,1,2,3}中任取一个元素,b从集合{0,1,2,3}中任取一个元素,求方程f(x)=0恰有两个不相等实根的概率;
(2)若b从区间[0,2]中任取一个数,a从区间[0,3]中任取一个数,求方程f(x)=0没有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数
B.?α,β∈R,使cos(α+β)=cosα+cosβ
C.向量 ![]() =(﹣2,1),
=(﹣2,1), ![]() =(﹣3,0),则
=(﹣3,0),则 ![]() 在
在 ![]() 方向上的投影为2
方向上的投影为2
D.“|x|≤1”是“x<1”的既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为1的正方形![]() 中,
中,![]() 分别为边
分别为边![]() 上的点,且
上的点,且![]() 的周长为2.
的周长为2.

(1)求线段![]() 长度的最小值;
长度的最小值;
(2)试探究![]() 是否为定值,若是,给出这个定值;若不是,说明理由.
是否为定值,若是,给出这个定值;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com