
| A. | 13 | B. | 17 | C. | 16 | D. | 19 |
分析 作出题中不等式组表示的平面区域,得如图的△ABC及其内部.根据题意z=$\overrightarrow{OA}$•$\overrightarrow{OM}$=3x+4y,将目标函数z=3x+4y对应的直线进行平移,由此可得本题的答案.
解答 解:∵点A坐标为(3,4),点M坐标为(x,y)
∴z=$\overrightarrow{OA}$•$\overrightarrow{OM}$=3x+4y,作出不等式组$\left\{\begin{array}{l}x+2y-5>0\\ 2x+y-7>0\\ x≥0\\ y≥0\end{array}\right.$表示的平面区域,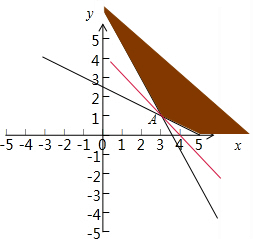
得到如图的区域,其中$\left\{\begin{array}{l}{2x+y-7=0}\\{x+2y-5=0}\end{array}\right.$,可得A(3,1),
将直线l:z=3x+4y进行平移,可得
当l经过点A时,目标函数z达到最小值,z最小值=3×3+4×1=13.
故选:A.
点评 本题给出二元一次不等式组,求目标函数z=$\overrightarrow{OA}$•$\overrightarrow{OM}$=3x+4y的取值范围,着重考查了向量的数量积、二元一次不等式组表示的平面区域和简单的线性规划等知识,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
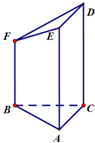 几何体ABCDEF如图所示,其中AC⊥AB,AC=3,AB=4,AE、CD、BF均垂直于面ABC,且AE=CD=5,BF=3,则这个几何体的体积为26.
几何体ABCDEF如图所示,其中AC⊥AB,AC=3,AB=4,AE、CD、BF均垂直于面ABC,且AE=CD=5,BF=3,则这个几何体的体积为26.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x<0”是“ln(x+1)<0”的充要条件 | |
| B. | “?x≥2,x2-3x+2≥0”的否定是“?x<2,x2-3x+2<0” | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60 | |
| D. | 已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程是$\widehat{y}$=1.23x+0.08 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com