
分析 利用整体构造思想,将cos(2α-$\frac{π}{6}$)=cos[(α+$\frac{π}{6}$)+(α-$\frac{π}{3}$)]利用诱导公式和同角三角函数关系即可求解.
解答 解:∵0$<α<\frac{π}{2}$,
∴$\frac{π}{6}<α+\frac{π}{6}<\frac{2π}{3}$,$-\frac{π}{3}<α-\frac{π}{3}<\frac{π}{6}$.
sin(α+$\frac{π}{6}$)=$\frac{3}{5}$
∵sin(α+$\frac{π}{6}$)=$\frac{3}{5}$$<\frac{\sqrt{3}}{2}$
故$a+\frac{π}{6}$$<\frac{π}{3}$,
∴$a<\frac{π}{6}$.
∴cos(α+$\frac{π}{6}$)=$\frac{4}{5}$;
又∵$-\frac{π}{3}<α-\frac{π}{3}<\frac{π}{6}$,sin(α+$\frac{π}{6}$)=cos[$\frac{π}{2}$-(α+$\frac{π}{6}$)]=cos(α$-\frac{π}{3}$)=$\frac{3}{5}$,
∴sin(α$-\frac{π}{3}$)=-$\frac{4}{5}$.
cos(2α-$\frac{π}{6}$)=cos[(α+$\frac{π}{6}$)+(α-$\frac{π}{3}$)]=cos(α+$\frac{π}{6}$)cos(α$-\frac{π}{3}$)-sin(α+$\frac{π}{6}$)sin(α$-\frac{π}{3}$)=$\frac{4}{5}$×$\frac{3}{5}$+$\frac{4}{5}×\frac{3}{5}$=$\frac{24}{25}$.
故答案为:0.
点评 本题考查两角和与差的公式的运用及计算能力,利用整体构造思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
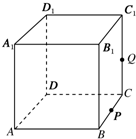 如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )
如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )| A. | ①③④ | B. | ②④⑤ | C. | ①②④ | D. | ①②③⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 17 | C. | 16 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<3} | B. | {x|1<x<3} | C. | {x|0<x<2} | D. | {x|1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com