
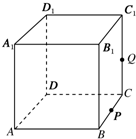
 如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )
如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )| A. | ①③④ | B. | ②④⑤ | C. | ①②④ | D. | ①②③⑤ |
分析 由已知情况根据CQ的不同取值,分别作出图形,利用数形结合思想能求出结果.
解答 解:当CQ=$\frac{1}{2}$时,S为等腰梯形,②正确,图如下: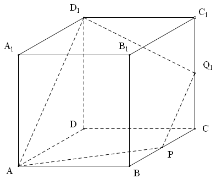
当CQ=1时,S是菱形,面积为$\sqrt{2}•\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}}{2}$,⑤正确,图如下: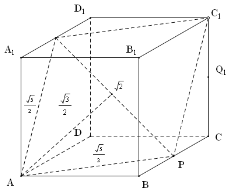
当CQ=$\frac{3}{4}$时,画图如下:C1R=$\frac{1}{3}$,③正确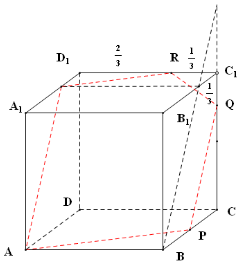
当$\frac{3}{4}<CQ<1$时,如图是五边形,④不正确;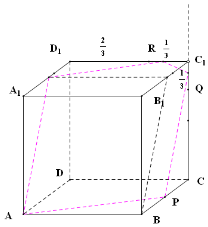
当0<CQ<$\frac{1}{2}$时,如下图,是四边形,故①正确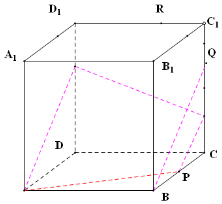
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意数形结合思想的合理运用.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| n | 二进制数 | an | n | 二进制数 | an | n | 二进制数 | an |
| 1 | 1 | 2 | 6 | 110 | 4 | 11 | 1011 | 8 |
| 2 | 10 | 2 | 7 | 111 | 8 | 12 | 1100 | 4 |
| 3 | 11 | 4 | 8 | 1000 | 2 | 13 | 1101 | 8 |
| 4 | 100 | 2 | 9 | 1001 | 4 | 14 | 1110 | 8 |
| 5 | 101 | 4 | 10 | 1010 | 4 | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com