
分析 (1)求出函数的导数,通过讨论a的范围,确定函数的单调区间即可;(2)先求出函数的导数,找到函数的极值点,从而证明出结论.
解答 解:(1)f′(x)=ex(x2+2x-a),
①当a≤-1时,f′(x)≥0,f(x)在R上递增;
②当a>-1时,令f′(x)=0,解得:${x_1}=-1-\sqrt{a+1},{x_2}=-1+\sqrt{a+1}$
∴f(x)的递增区间为(-∞,x1),(x2,+∞),减区间为(x1,x2);
(2)f′(x)=ex(x2+2x-a).
因为函数f(x)有两个不同的零点,即f′(x)有两个不同的零点,
即方程x2+2x-a=0的判别式△=4+4a>0,解得:a>-1,
由x2+2x-a=0,解得x1=-1-$\sqrt{a+1}$,x2=-1+$\sqrt{a+1}$,
此时x1+x2=-2,x1•x2=-a,
随着x变化,f(x)和f′(x)的变化情况如下:
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
点评 本题考查了函数的单调性,函数的极值问题,导数的应用,考查转化思想,分类讨论思想,熟练掌握基础知识并对其灵活应用是解题的关键,本题是一道难题.


科目:高中数学 来源: 题型:选择题
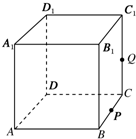 如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )
如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )| A. | ①③④ | B. | ②④⑤ | C. | ①②④ | D. | ①②③⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<3} | B. | {x|1<x<3} | C. | {x|0<x<2} | D. | {x|1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com