Question

16．记集合$A=\left\{（x，y）|{x}^{2}+{y}^{2}≤1\right\}，B=\{（x，y）|\left\{\begin{array}{l}x+y≤1\\ x≥0\\ y≥0\end{array}\right.\}$，构成的平面区域分别为M，N，现随机地向M中抛一粒豆子（大小忽略不计），则该豆子落入N中的概率为$\frac{1}{2π}$．

Answer 1

分析 平面区域M、N，分别为圆与直角三角形，面积分别为π，$\frac{1}{2}$，利用几何概型的概率公式解之即可．

解答 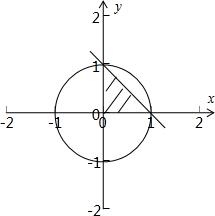解：集合$A=\{（x，y）|{x}^{2}+{y}^{2}≤1\}，B=\left\{（x，y）|\left\{\begin{array}{l}x+y≤1\\ x≥0\\ y≥0\end{array}\right\}$构成的平面区域M、N，分别为圆与直角三角形，
面积分别为π，$\frac{1}{2}$，随机地向M中抛一粒豆子（大小忽略不计），则该豆子落入N中的概率为$\frac{\frac{1}{2}}{π}$=$\frac{1}{2π}$．
答案为：$\frac{1}{2π}$．

点评 本题主要考查了几何概型的概率，确定区域面积是关键，属于中档题．