
| A. | $3021+\sqrt{3}$ | B. | $3024+\sqrt{3}$ | C. | $3021+\frac{{\sqrt{3}-1}}{2}$ | D. | $3024+\frac{{\sqrt{3}-1}}{2}$ |
分析 通过写出前几项,寻找他们之间的规律,归纳得出结论.
解答 解:a1=$\sqrt{3}$,
a2=1+$\frac{1}{\sqrt{3}-1}$=$\frac{3}{2}$+$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$(3+$\sqrt{3}$),
a3=2+$\frac{1}{\frac{\sqrt{3}}{2}-\frac{1}{2}}$=3+$\sqrt{3}$=a1+3,
a4=4+$\frac{1}{\sqrt{3}-1}$=a2+3,
a5=5+$\frac{1}{\frac{\sqrt{3}}{2}-\frac{1}{2}}$=a3+3=a1+6,
…
∴a2017=a2015+3=a2013+6=…=a1+3×($\frac{2017-1}{2}$)=3024+$\sqrt{3}$.
故选:B.
点评 本题考查了数列递推关系、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | (¬p)∧(¬q) | D. | (¬p)∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-2 | B. | a>-2 | C. | a<-9 | D. | a>-9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{15}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
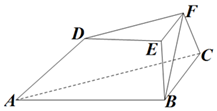 如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com