
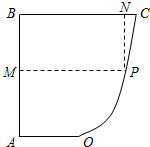
 如图所示,已知AB⊥BC,OA∥BC,且AB=BC=2OA=4,曲线段OC是以点O为顶点且对称轴与AB平行的抛物线的一段.设P是曲线段OC上任意一点,点M在AB上,点N在BC上,PMBN是矩形,问点P在曲线段OC上什么位置的时候才能使矩形PMBN的面积最大?并求出最大面积.
如图所示,已知AB⊥BC,OA∥BC,且AB=BC=2OA=4,曲线段OC是以点O为顶点且对称轴与AB平行的抛物线的一段.设P是曲线段OC上任意一点,点M在AB上,点N在BC上,PMBN是矩形,问点P在曲线段OC上什么位置的时候才能使矩形PMBN的面积最大?并求出最大面积. 分析 建立直角坐标系,求得C点坐标,设抛物线方程,将P代入抛物线方程,求得a,求得抛物线方程,求得矩形PMBN的面积S的表达式,求导,根据函数的单调性,当$x=\frac{2}{3}$时,S取得最大值,即$|{PN}|=\frac{32}{9}$,矩形PMBN面积的最大值为$\frac{256}{27}$.
解答 解:以O为原点,AO所在直线为x轴建立如图所示的直角坐标系.依题意,C(2,4),…(2分)
设曲线段所对应的抛物线方程为y=ax2,
∵P在曲线段OC上,
∴4=a×22,a=1,…(4分)
抛物线方程为y=x2(0≤x≤2),
设P(x,x2)(0≤x≤2)是曲线段上任意一点,则|PM|=x+2,|PN|=4-x2,
所以${S_{PMBN}}=(2+x)(4-{x^2})=8+4x-2{x^2}-{x^3}(0≤x<2)$,…(8分)
S'=-3x2-4x+4=-(3x-2)(x+2),…(10分)
当$-2<x<\frac{2}{3}$时,S'>0;当$x>\frac{2}{3}$时,S'<0,
∴在区间$[0\;,\;\frac{2}{3})$上,S是x的增函数,
在区间$(\frac{2}{3}\;,\;2)$上,S是x的减函数,…(12分)
∴当$x=\frac{2}{3}$时,S取得最大值,此时$|{PN}|=\frac{32}{9}$,…(13分)
即点P在曲线段OC上,到BC的距离为$\frac{32}{9}$时,矩形PMBN面积的最大值为$\frac{256}{27}$.…(14分)
点评 本题考查抛物线的标准方程,利用导数求函数的单调性及最值,考查计算能力,属于中档题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:填空题
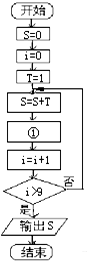 如图是在求:S=1+$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+的一个程序框图.
如图是在求:S=1+$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+的一个程序框图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>a>c | C. | c>a>b | D. | a>b>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com