
分析 首先,根据直线l的参数方程为$\left\{\begin{array}{l}{x=2+2t}\\{y=1-t}\end{array}\right.$(t为参数),化简为普通方程为:x+2y=4,然后,设P(2cosθ,sinθ),根据点到直线的距离求解即可.
解答 解:根据直线l的参数方程为$\left\{\begin{array}{l}{x=2+2t}\\{y=1-t}\end{array}\right.$(t为参数),得其普通方程为:x+2y=4,
设P(2cosθ,sinθ),
∴P到l的距离为d=$\frac{|2cosθ+2sinθ-4|}{\sqrt{5}}$=$\frac{|2\sqrt{2}sin(θ+\frac{π}{4})-4|}{\sqrt{5}}$≥$\frac{4-2\sqrt{2}}{\sqrt{5}}$,
当且仅当sin(θ+$\frac{π}{4}$)=1,即θ=2kπ+$\frac{π}{4}$时等号成立.
此时,sinθ=cosθ=$\frac{\sqrt{2}}{2}$,
∴P($\sqrt{2}$,$\frac{\sqrt{2}}{2}$).
点评 本题重点考查了参数方程和普通的互化、点到直线的距离公式等知识,属于中档题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,c=0,则ac>bc | B. | 若ac2>bc2,则a>b | ||
| C. | 若a>b,则$\frac{1}{a}$>$\frac{1}{b}$ | D. | 若a>b,则ac2>bc2 | ||
| E. | 若a>b,则ac2>bc2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
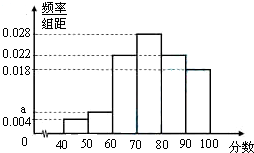 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]查看答案和解析>>
科目:高中数学 来源: 题型:解答题
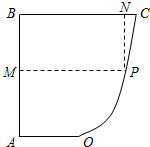 如图所示,已知AB⊥BC,OA∥BC,且AB=BC=2OA=4,曲线段OC是以点O为顶点且对称轴与AB平行的抛物线的一段.设P是曲线段OC上任意一点,点M在AB上,点N在BC上,PMBN是矩形,问点P在曲线段OC上什么位置的时候才能使矩形PMBN的面积最大?并求出最大面积.
如图所示,已知AB⊥BC,OA∥BC,且AB=BC=2OA=4,曲线段OC是以点O为顶点且对称轴与AB平行的抛物线的一段.设P是曲线段OC上任意一点,点M在AB上,点N在BC上,PMBN是矩形,问点P在曲线段OC上什么位置的时候才能使矩形PMBN的面积最大?并求出最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,2)∪(2,+∞) | C. | (-$\frac{1}{2}$,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5}{14}$,$\frac{9+\sqrt{21}}{40}$) | B. | $\frac{5}{14}$ | C. | ($\frac{5}{12}$,$\frac{1}{2}$) | D. | ($\frac{5}{14}$,$\frac{5}{12}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com