
| A. | ($\frac{5}{14}$,$\frac{9+\sqrt{21}}{40}$) | B. | $\frac{5}{14}$ | C. | ($\frac{5}{12}$,$\frac{1}{2}$) | D. | ($\frac{5}{14}$,$\frac{5}{12}$) |
分析 将问题转化为y=f(x)与y=k(x+1)有6个交点,作出函数图象,求出两函数图象恰有5个交点和7个交点时的k值,即可得出k的范围.
解答 解:令g(x)=0得f(x)=k(x+1).
作出y=f(x)与y=k(x+1)的函数图象,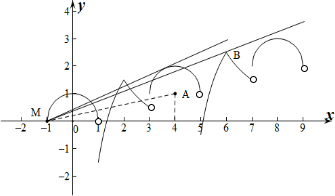
由图象可知M(-1,0)为两函数图象的一个交点.
当直线y=k(x+1)与f(x)在[3,4)上的函数图象相切时,两函数图象有恰好有5个交点,
设此时直线斜率为k1,A(4,1),则tan∠AMx=$\frac{1}{5}$,
∴k1=tan2∠AMx=$\frac{2tan∠AMx}{1-ta{n}^{2}∠AMx}$=$\frac{5}{12}$.
设B(6,$\frac{5}{2}$),则当直线y=k(x+1)经过点B时,两函数图象恰好有7个交点,
设此时直线斜率为k2,则k2=kBM=$\frac{\frac{5}{2}-0}{6+1}$=$\frac{5}{14}$.
∴k的取值范围是($\frac{5}{14}$,$\frac{5}{12}$).
点评 本题考查了函数零点个数与函数图象的关系,准确作出函数图象,寻找k的临界值是解题的关键,属于中档题.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-7=0 | B. | 2x-y-7=0 | C. | 2x+y+7=0 | D. | 2x-y+7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>a>c | C. | c>a>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com