
分析 a=1时,不等式不可能恒成立;a≠1,若对任意的x>0时均有[(a-1)x-1]•(x2-ax-1)≥0,则函数y1=(a-1)x-1,y2=x2-ax-1,与x轴交于同一点,代入可得答案.
解答 解:(1)a=1时,代入题中不等式明显不恒成立.
(2)a≠1,构造函数y1=(a-1)x-1,y2=x2-ax-1,它们都过定点P(0,-1).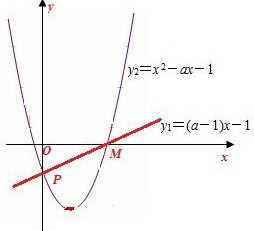
考查函数y1=(a-1)x-1:
令y=0,得M($\frac{1}{a-1}$,0),
∴a>1;
考查函数y2=x2-ax-1,
∵x>0时均有[(a-1)x-1](x2-ax-1)≥0,
∴y2=x2-ax-1过点M($\frac{1}{a-1}$,0),代入得:($\frac{1}{a-1}$)2-a•$\frac{1}{a-1}$-1=0,
解之得:a=$\frac{3}{2}$,或a=0(舍去).
故答案为:$\frac{3}{2}$
点评 本题考查的知识点为函数恒成立问题,函数的图象和性质,分类讨论思想,数形结合思想,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
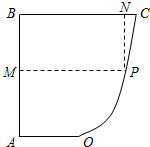 如图所示,已知AB⊥BC,OA∥BC,且AB=BC=2OA=4,曲线段OC是以点O为顶点且对称轴与AB平行的抛物线的一段.设P是曲线段OC上任意一点,点M在AB上,点N在BC上,PMBN是矩形,问点P在曲线段OC上什么位置的时候才能使矩形PMBN的面积最大?并求出最大面积.
如图所示,已知AB⊥BC,OA∥BC,且AB=BC=2OA=4,曲线段OC是以点O为顶点且对称轴与AB平行的抛物线的一段.设P是曲线段OC上任意一点,点M在AB上,点N在BC上,PMBN是矩形,问点P在曲线段OC上什么位置的时候才能使矩形PMBN的面积最大?并求出最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,10) | C. | (1,+∞) | D. | (10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com