
分析 根据题设条件,利用导数先求出切线方程,进而求出xn,从而得到an,再由对数的运算法则能求出结果.
解答 解:∵曲线y=2015xn+1(n∈N*),
∴y′=2015(n+1)xn,
∴y′|x=1=2015(n+1),
∴曲线y=2015xn+1(n∈N*)在点(1,2015)处的切线方程为:
y-2015=2015(n+1)(x-1),
令y=0,解得切线与x轴的交点的横坐标为xn=x=$\frac{n}{n+1}$,
∵an=log2015xn=log2015$\frac{n}{n+1}$,
∴a1+a2+…+a2014
=log2015$\frac{1}{2}$+log2015$\frac{2}{3}$+…+log2015$\frac{2014}{2015}$
=log2015($\frac{1}{2}$×$\frac{2}{3}$×…×$\frac{2014}{2015}$)
=-1.
故答案为:-1.
点评 本题考查数列求和,涉及到导数、对数、数列等知识点,是一道构思巧妙的好题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
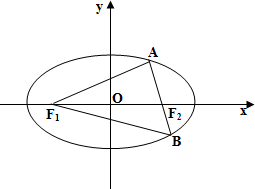 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,离心率e=$\frac{1}{2}$,F1,F2分别为左、右焦点,AB是过右焦点的弦.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,离心率e=$\frac{1}{2}$,F1,F2分别为左、右焦点,AB是过右焦点的弦.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com