
分析 (1)当a=$\frac{1}{2}$时,原不等式等价于(2x-1)(x-2)≤0,解得即可,
(2)当a>0时,x2-(a+$\frac{1}{a}$)x+1≤0等价于(x-a)(x-$\frac{1}{a}$)≤0,对a进行分类讨论即可.
解答 解:(1)a=$\frac{1}{2}$时,f(x)≤0,即x2-$\frac{5}{2}$x+1≤0,
即2x2-5x+2≤0,即(2x-1)(x-2)≤0,解得$\frac{1}{2}$≤x≤2,
故不等式的解集为[$\frac{1}{2}$,2];
(2)当a>0时,x2-(a+$\frac{1}{a}$)x+1≤0等价于(x-a)(x-$\frac{1}{a}$)≤0
①若0<a<1,解得:a≤x≤$\frac{1}{a}$,故其解集为[a,$\frac{1}{a}$]
②若a=1,解得:x=1;故其解集为{1},
③若a>1,解得:$\frac{1}{a}$≤x≤a,故其解集为[$\frac{1}{a}$,a].
点评 本题考查了分类讨论、一元二次不等式的解法、一元二次方程的解法等基础知识与基本技能方法,属于中档题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,10) | C. | (1,+∞) | D. | (10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
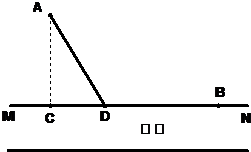 有一条笔直的河流,仓库A到河岸所在直线MN的距离是10km,AC⊥MN于C,码头B到C的距离为20km.现有一批货物要从A运到B.已知货物走陆路时,单位里程的运价是水路的2倍,货物走陆路到达D后再由水路到达B,问点D应选在离C多远处才能使总运费最低?
有一条笔直的河流,仓库A到河岸所在直线MN的距离是10km,AC⊥MN于C,码头B到C的距离为20km.现有一批货物要从A运到B.已知货物走陆路时,单位里程的运价是水路的2倍,货物走陆路到达D后再由水路到达B,问点D应选在离C多远处才能使总运费最低?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com