
分析 (1)先根据分层抽样的规则,求出每组应抽取2名学生.
(II)从甲组抽取的学生中恰有1名女生的事件应该是甲组一名女生,已组一名男生.
(III)本事件可以按从甲组中抽取的男人数进行分类:第一类是甲组两男乙组两女;第二类是甲组一男一女乙组一男一女;第三类是甲组二女乙组两男,
解答 解:( I)由于甲、乙两组各有10名学生,
根据分层抽样原理,要从甲、乙两组中共抽取4名学生进行面试,则从每组各抽取2名学生.
( II)记A表示事件:从甲组抽取的学生中恰有1名女学生,则$P(A)=\frac{C_4^1C_6^1}{{C_{10}^2}}=\frac{8}{15}$;
( III)Ai表示事件:从甲组抽取的2名学生中恰有i名男学生,i=0,1,2,Bj表示事件:
从乙组抽取的2名学生中恰有j名男学生,j=0,1,2,
B表示事件:抽取的4名学生中恰有2名男学生.Ai与Bj独立,i,j=0,1,2,
且B=A0•B2+A1•B1+A2•B0;
故P(B)=P(A0•B2+A1•B1+A2•B0)
=P(A0)•P(B2)+P(A1)•P(B1)+P(A2)•P(B0)
=$\frac{C_4^2}{{C_{10}^2}}•\frac{C_4^2}{{C_{10}^2}}+\frac{C_4^1C_6^1}{{C_{10}^2}}•\frac{C_6^1C_4^1}{{C_{10}^2}}+\frac{C_6^2}{{C_{10}^2}}•\frac{C_6^2}{{C{\;}_{10}^2}}$=$\frac{93}{225}$.
即 P(B)=$\frac{93}{225}$.
点评 本题考查分层抽样以及古典概型的应用,是基本知识的考查.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
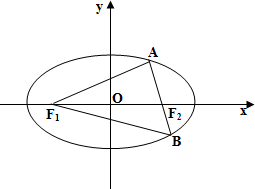 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,离心率e=$\frac{1}{2}$,F1,F2分别为左、右焦点,AB是过右焦点的弦.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,离心率e=$\frac{1}{2}$,F1,F2分别为左、右焦点,AB是过右焦点的弦.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 95 | B. | 105 | C. | 840 | D. | 760 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=4sin(4x+$\frac{π}{6}$) | B. | y=4sin(4x+$\frac{π}{3}$) | C. | y=2sin(4x+$\frac{π}{3}$) | D. | y=2sin(4x+$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com