
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\frac{2\sqrt{3}}{3}$ | D. | 2 |
分析 由$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,向量$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,可得$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.由向量$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,向量$\overrightarrow{a}$,$\overrightarrow{b}$均为单位问量由向量夹角为$\frac{π}{6}$,可得∠ACB=$\frac{π}{6}$.由等边三角形OAB,点C在AB外且∠ACB为定值,可得C的轨迹是两段圆弧,∠ACB是AB所对的圆周角.因此:当AC时是弧 $\widehat{AB}$所在圆(上述圆弧)的直径时,|$\overrightarrow{a}$-$\overrightarrow{c}$|取得最大值|AC|.
解答 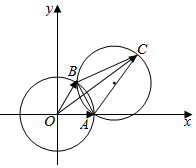 解:∵由$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,向量$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,可得$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.由向量$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,向量$\overrightarrow{a}$,$\overrightarrow{b}$均为单位问量
解:∵由$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,向量$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,可得$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.由向量$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,向量$\overrightarrow{a}$,$\overrightarrow{b}$均为单位问量
∴1×1×cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,
∴$<\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.
设 $\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.
∵向量 $\overrightarrow{c}$满足 $\overrightarrow{a}$-$\overrightarrow{c}$与 $\overrightarrow{b}$-$\overrightarrow{c}$的夹角为 $\frac{π}{6}$,
∴∠ACB=$\frac{π}{6}$.
由等边三角形OAB,点C在AB外且∠ACB为定值,可得C的轨迹是两段圆弧,∠ACB是AB所对的圆周角.
可知:当AC时是弧 $\widehat{AB}$所在圆(上述圆弧)的直径时,|$\overrightarrow{a}$-$\overrightarrow{c}$|取得最大值|AC|,
在△ABC中,由正弦定理可得:AC=$\frac{AB}{sin30°}$=2.
∴|,|$\overrightarrow{a}$-$\overrightarrow{c}$|取得最大值|AC|取得最大值是2.
故选:D.
点评 本题考查了向量的数量积运算性质、向量的减法运算及其几何意义、圆的性质、直角三角形的边角关系,考查了数形结合的思想方法、推理能力与计算能力,属于难题


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{6}$,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{5π}{6}$] | C. | [-$\frac{5π}{12}$,$\frac{π}{12}$] | D. | [$\frac{π}{12}$,$\frac{7π}{12}$]] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
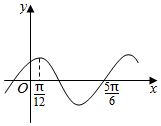 设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0),且函数f(x)的部分图象如图所示,则有( )
设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0),且函数f(x)的部分图象如图所示,则有( )| A. | f(-$\frac{3π}{4}$)<f($\frac{5π}{3}$)<f($\frac{7π}{6}$) | B. | f(-$\frac{3π}{4}$)<f($\frac{7π}{6}$)<f($\frac{5π}{3}$) | C. | f($\frac{5π}{3}$)<f($\frac{7π}{6}$)<f(-$\frac{3π}{4}$) | D. | f($\frac{5π}{3}$)<f(-$\frac{3π}{4}$)<f($\frac{7π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com