
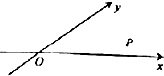
 如图,a∈(0,π),且a≠$\frac{π}{2}$,当∠xOy=e时,定义平面坐标系xOy为a仿射坐标系,在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y),若在仿射坐标系中,已知$\overrightarrow{a}$=(m,n),$\overrightarrow{b}$=(s,t),下列结论中不正确的是( )
如图,a∈(0,π),且a≠$\frac{π}{2}$,当∠xOy=e时,定义平面坐标系xOy为a仿射坐标系,在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y),若在仿射坐标系中,已知$\overrightarrow{a}$=(m,n),$\overrightarrow{b}$=(s,t),下列结论中不正确的是( )| A. | 若$\overrightarrow{a}$=$\overrightarrow{b}$,则m=s,n=t | |
| B. | 若$\overrightarrow{a}$$∥\overrightarrow{b}$,则mt-ns=0 | |
| C. | 若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则ms+nt=0 | |
| D. | 若m=t=1,n=s=2,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角$\frac{π}{3}$,则a=$\frac{2π}{3}$ |
分析 根据在仿射坐标系中斜坐标的定义,便可得到$\overrightarrow{a}=m\overrightarrow{{e}_{1}}+n\overrightarrow{{e}_{2}},\overrightarrow{b}=s\overrightarrow{{e}_{1}}+t\overrightarrow{{e}_{2}}$,然后由平面向量基本定理及共线向量基本定理,以及向量垂直的充要条件,向量夹角的余弦公式即可判断每项结论的正误.
解答 解:根据斜坐标的定义,$\overrightarrow{a}=(m,n),\overrightarrow{b}=(s,t)$;
∴$\overrightarrow{a}=m\overrightarrow{{e}_{1}}+n\overrightarrow{{e}_{2}},\overrightarrow{b}=s\overrightarrow{{e}_{1}}+t\overrightarrow{{e}_{2}}$;
A.若$\overrightarrow{a}=\overrightarrow{b}$,根据平面向量基本定理得:m=s,n=t,∴该结论正确;
B.若$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在实数k,使$\overrightarrow{b}=k\overrightarrow{a}$,$k\overrightarrow{a}=mk\overrightarrow{{e}_{1}}+nk\overrightarrow{{e}_{2}}$;
∴$\left\{\begin{array}{l}{s=mk}\\{t=nk}\end{array}\right.$;
∴$\frac{s}{m}=\frac{t}{n}$;
∴mt-ns=0;
∴该结论正确;
C.若$\overrightarrow{a}⊥\overrightarrow{b}$,则:$\overrightarrow{a}•\overrightarrow{b}=(m\overrightarrow{{e}_{1}}+n\overrightarrow{{e}_{2}})•(s\overrightarrow{{e}_{1}}+t\overrightarrow{{e}_{2}})$=$ms+(mt+ns)\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+nt=0$;
$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}≠0$;
∴ms+nt≠0;
∴该结论错误;
D.若m=t=1,n=s=2,$\overrightarrow{a}=\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}},\overrightarrow{b}=2\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}}$,$\overrightarrow{a},\overrightarrow{b}$的夹角为$\frac{π}{3}$,则:$cos\frac{π}{3}=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$;
$\overrightarrow{a}•\overrightarrow{b}=2+5\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+2=4+5cosa$,$|\overrightarrow{a}|=\sqrt{{\overrightarrow{a}}^{2}}=\sqrt{5+4cosa}$,$|\overrightarrow{b}|=\sqrt{{\overrightarrow{b}}^{2}}=\sqrt{5+4cosa}$;
∴$\frac{1}{2}=\frac{4+5cosa}{5+4cosa}$;
解得$cosα=-\frac{1}{2}$;
∴$a=\frac{2π}{3}$;
∴该结论正确.
故选:C.
点评 考查对仿射坐标系的理解,及对定义的斜坐标的理解,以及平面向量基本定理、共面向量基本定理,向量垂直的充要条件,向量夹角的余弦公式.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)的假设正确,(2)的假设错误 | B. | (1)与(2)的假设都正确 | ||
| C. | (1)的假设错误,(2)的假设正确 | D. | (1)与(2)的假设都错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 19 | B. | 18 | C. | 17 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,使得ex≤1 | B. | ?x≤0,使得ex<1 | C. | ?x>0,使得ex<1 | D. | ?x>0,使得ex≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{3}$,$\sqrt{3}$) | B. | (-2,2) | C. | (0,2) | D. | (-∞,-2),(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com