练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某地发生地质灾害，使当地的自来水受到了污染，某部门对水质检测后，决定往水中投放一种药剂来净化水质．已知每投放质量为m的药剂后，经过x天该药剂在水中释放的浓度y（毫克/升）满足，其中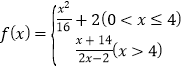，当药剂在水中释放的浓度不低于4（毫克/升）时称为有效净化；当药剂在水中释放的浓度不低于4（毫克/升）且不高于10（毫克/升）时称为最佳净化．

    （1）如果投放的药剂质量为m=4，试问自来水达到有效净化一共可持续几天？

    （2）如果投放的药剂质量为m，为了使在7天（从投放药剂算起包括7天）之内的自来水达到最佳净化，试确定应该投放的药剂质量m的最小值．

    【答案】（1）16天（2）

    【解析】

    (1)由题意首先得到该药剂在水中释放的浓度的解析式，然后求解不等式即可确定自来水达到有效净化一共可持续的天数.

    （2）由确定各段的单调性，求出值域，然后将原问题转化为恒成立的问题可得m的最小值.

    （1）由题意，当药剂质量为m=4，所以

    当时，显然符合题意．
    当x＞4时，解得，

    综上，

    所以自来水达到有效净化一共可持续16天．
    （2）由，得：

    在区间（0，4]上单调递增，即；
    在区间（4，7]上单调递减，即，
    综上，
    为使恒成立，只要且即可，

    即所以应该投放的药剂质量m的最小值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若函数在上单调递减，求实数的取值范围；

    （2）是否存在实数，使得在上的值域恰好是？若存在，求出实数的值；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点O是四边形内一点，判断结论：“若，则该四边形必是矩形，且O为四边形的中心”是否正确，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在空间四边形中，， ，，，且平面平面.

    （1）求证：；

    （2）若直线与平面所成角的余弦值为，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是一几何体的平面展开图，其中四边形ABCD为矩形，E，F分别为PA，PD的中点，在此几何体中，给出下面4个结论：

    直线BE与直线CF异面；直线BE与直线AF异面；直线平面PBC；平面平面PAD．

    其中正确的结论个数为　　

    A. 4个

    B. 3个

    C. 2个

    D. 1个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】判断下列函数的奇偶性：

    （1）f(x)＝|x－2|＋|x＋2|；

    （2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知长度为的线段的两个端点、分别在轴和轴上运动，动点满足，设动点的轨迹为曲线.

    （1）求曲线的方程；

    （2）过点且斜率不为零的直线与曲线交于两点、，在轴上是否存在定点，使得直线与的斜率之积为常数.若存在，求出定点的坐标以及此常数；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线y=x2+mx–2与x轴交于A，B两点，点C的坐标为(0,1).当m变化时，解答下列问题：

    （1）能否出现AC⊥BC的情况？说明理由；

    （2）证明过A，B，C三点的圆在y轴上截得的弦长为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (I) 当时，求函数的单调区间;

    (II) 当时，恒成立，求的取值范围.

    查看答案和解析>>

    同步练习册答案