练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】判断下列函数的奇偶性：

    （1）f(x)＝|x－2|＋|x＋2|；

    （2）

    【答案】（1）偶函数；（2）偶函数.

    【解析】

    （1）先求得函数的定义域，然后由判断出为偶函数.

    （2）先判断的定义域关于原点对称，然后利用分段的方法，证得，由此判断出为偶函数.

    （1）函数f(x)＝|x－2|＋|x＋2|的定义域为R.

    因对于任意的x∈R，都有f(－x)＝|－x－2|＋|－x＋2|＝|x＋2|＋|x－2|＝f(x)，所以函数f(x)＝|x－2|＋|x＋2|是偶函数．

    （2）函数的定义域为(－∞，0)∪(0，＋∞)，关于原点对称．

    当x>0时，－x<0，则f(－x)＝＝＝f(x)；

    当x<0时，－x>0，则f(－x)＝＝＝f(x)．

    综上可知是偶函数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

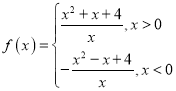
    科目：高中数学 来源： 题型：

    【题目】袋中有7个球，其中4个白球，3个红球，从袋中任意取出2个球，求下列事件的概率：

    (1) 取出的2个球都是白球；

    (2)取出的2个球中1个是白球，另1个是红球．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现从某医院中随机抽取了七位医护人员的关爱患者考核分数（患者考核： 分制），用相关的特征量表示；医护专业知识考核分数（试卷考试： 分制），用相关的特征量表示，数据如下表：

    特征量

    1

    2

    3

    4

    5

    6

    7

    98

    88

    96

    91

    90

    92

    96

    9.9

    8.6

    9.5

    9.0

    9.1

    9.2

    9.8

    （1）求关于的线性回归方程（计算结果精确到）；

    （2）利用（1）中的线性回归方程，分析医护专业考核分数的变化对关爱患者考核分数的影响，并估计某医护人员的医护专业知识考核分数为分时，他的关爱患者考核分数（精确到）；

    （3）现要从医护专业知识考核分数分以下的医护人员中选派人参加组建的“九寨沟灾后医护小分队”培训，求这两人中至少有一人考核分数在分以下的概率.

    附：回归方程中斜率和截距的最小二乘法估计公式分别为， .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆的方程为：．

    （1）直线过点，且与圆交于两点，若，求直线的方程；

    （2）圆上有一动点，，若向量，求动点的轨迹方程，并说明此轨迹是什么曲线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地发生地质灾害，使当地的自来水受到了污染，某部门对水质检测后，决定往水中投放一种药剂来净化水质．已知每投放质量为m的药剂后，经过x天该药剂在水中释放的浓度y（毫克/升）满足，其中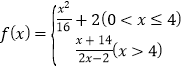，当药剂在水中释放的浓度不低于4（毫克/升）时称为有效净化；当药剂在水中释放的浓度不低于4（毫克/升）且不高于10（毫克/升）时称为最佳净化．

    （1）如果投放的药剂质量为m=4，试问自来水达到有效净化一共可持续几天？

    （2）如果投放的药剂质量为m，为了使在7天（从投放药剂算起包括7天）之内的自来水达到最佳净化，试确定应该投放的药剂质量m的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）若函数f(x)＝ax2＋bx＋3a＋b是偶函数，定义域为[a－1，2a]，则a＝________，b＝________；

    （2）已知函数f(x)＝ax2＋2x是奇函数，则实数a＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某生物研究者于元旦在湖中放入一些凤眼莲，这些凤眼莲在湖中的蔓延速度越来越快，二月底测得凤眼莲覆盖面积为，三月底测得凤眼莲覆盖面积为，凤眼莲覆盖面积 （单位：）与月份（单位：月）的关系有两个函数模型与可供选择.

    （1）试判断哪个函数模型更合适并求出该模型的解析式；

    （2）求凤眼莲覆盖面积是元旦放入面积倍以上的最小月份.

    （参考数据，）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为鼓励家校互动,与某手机通讯商合作,为教师办理流量套餐.为了解该校教师手机流量使用情况,通过抽样,得到位教师近年每人手机月平均使用流量(单位:)的数据,其频率分布直方图如下：

    若将每位教师的手机月平均使用流量分别视为其手机月使用流量,并将频率为概率,回答以下问题.

    (Ⅰ) 从该校教师中随机抽取人,求这人中至多有人月使用流量不超过 的概率；

    (Ⅱ) 现该通讯商推出三款流量套餐,详情如下:

    套餐名称

    月套餐费(单位:元)

    月套餐流量(单位:)

    这三款套餐都有如下附加条款:套餐费月初一次性收取,手机使用一旦超出套餐流量,系统就自动帮用户充值 流量,资费元；如果又超出充值流量,系统就再次自动帮用户充值 流量,资费元/次,依次类推,如果当月流量有剩余,系统将自动清零,无法转入次月使用.

    学校欲订购其中一款流量套餐,为教师支付月套餐费,并承担系统自动充值的流量资费的,其余部分由教师个人承担,问学校订购哪一款套餐最经济？说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】抛物线顶点在原点，焦点在x轴上，且过点（4，4），焦点为F．

    （1）求抛物线的焦点坐标和标准方程；

    （2）P是抛物线上一动点，M是PF的中点，求M的轨迹方程．

    查看答案和解析>>

    同步练习册答案