考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)f′(x)=k-e
x,x∈R,对k分类讨论即可得出.
(Ⅱ)不等式f(x)≥g(x)-e
x在区间(0,+∞)上恒成立,则
kx≥,可得
k≥.令h(x)=
,则不等式f(x)≥g(x)-e
x在区间(0,+∞)上恒成立?k≥h(x)
max.利用导数研究函数的单调性即可得出.
(III)由(Ⅱ)知:
≤,
<•,(x≥2).令x=n,则
<•<(-).
“累加求和”即可得出.
解答:
解:(Ⅰ)∵f′(x)=k-e
x,x∈R,∴f′(x)=0得e
x=k.
当k≤0时,f′(x)<0,f(x)在R上单调递减;
当k>0时,令f′(x)=0得x=lnk
由f′(x)>0的f(x)的单调递增区间为(-∞,lnk);
由f′(x)<0的f(x)的单调递减区间为(lnk,+∞).
(Ⅱ)不等式f(x)≥g(x)-e
x在区间(0,+∞)上恒成立,则
kx≥,可得
k≥.
令h(x)=
,则不等式f(x)≥g(x)-e
x在区间(0,+∞)上恒成立?k≥h(x)
max.
令h′(x)=
=0,解得x=
.
列表如下:
| x | (0,) | | (,+∞) |
| h′(x) | + | 0 | - |
| h(x) | 单调递增 | 极大值 | 单调递减 |
由表格可知:当x=
时,函数h(x)有极大值即最大值,且
h()=
.
因此k
≥.
(Ⅲ)证明:由(Ⅱ)知:
≤,∴
<•,(x≥2).
令x=n,则
<•<(-).
∴
++…+<[(1-)+(-)+…+
(-)]=
(1-)<.
点评:本题综合考查了利用导数研究函数的单调性、极值与最值,考查了“累加求和”、“裂项求和”方法,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.



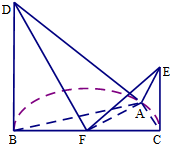 如图,BC是半圆F的直径,点A在半圆F上,BC=4
如图,BC是半圆F的直径,点A在半圆F上,BC=4