
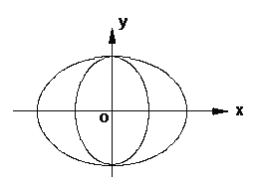
【题目】如图,曲线![]() 由两个椭圆
由两个椭圆![]() :
:![]() 和椭圆
和椭圆![]() :
:![]() 组成,当
组成,当![]() 成等比数列时,称曲线
成等比数列时,称曲线![]() 为“猫眼曲线”.
为“猫眼曲线”.
(1)若猫眼曲线![]() 过点
过点![]() ,且
,且![]() 的公比为
的公比为![]() ,求猫眼曲线
,求猫眼曲线![]() 的方程;
的方程;
(2)对于题(1)中的求猫眼曲线![]() ,任作斜率为
,任作斜率为![]() 且不过原点的直线与该曲线相交,交椭圆
且不过原点的直线与该曲线相交,交椭圆![]() 所得弦的中点为M,交椭圆
所得弦的中点为M,交椭圆![]() 所得弦的中点为N,求证:
所得弦的中点为N,求证:![]() 为与
为与![]() 无关的定值;
无关的定值;
(3)若斜率为![]() 的直线
的直线![]() 为椭圆
为椭圆![]() 的切线,且交椭圆
的切线,且交椭圆![]() 于点
于点![]() ,
,![]() 为椭圆
为椭圆![]() 上的任意一点(点
上的任意一点(点![]() 与点
与点![]() 不重合),求
不重合),求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的右焦点与短轴两端点构成一个面积为
的右焦点与短轴两端点构成一个面积为![]() 的等腰直角三角形,
的等腰直角三角形,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)设点![]() 在椭圆
在椭圆![]() 上运动,
上运动,![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为常数
的距离为常数![]()
![]() ,求动点
,求动点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为p,公差为
的首项为p,公差为![]() ,对于不同的自然数
,对于不同的自然数![]() ,直线
,直线![]() 与
与![]() 轴和指数函数
轴和指数函数![]() 的图象分别交于点
的图象分别交于点![]() 与
与![]() (如图所示),记
(如图所示),记![]() 的坐标为
的坐标为![]() ,直角梯形
,直角梯形![]() 、
、![]() 的面积分别为
的面积分别为![]() 和
和![]() ,一般地记直角梯形
,一般地记直角梯形![]() 的面积为
的面积为![]() .
.

(1)求证:数列![]() 是公比绝对值小于1的等比数列;
是公比绝对值小于1的等比数列;
(2)设![]() 的公差
的公差![]() ,是否存在这样的正整数
,是否存在这样的正整数![]() ,构成以
,构成以![]() ,
,![]() ,
,![]() 为边长的三角形?并请说明理由;
为边长的三角形?并请说明理由;
(3)设![]() 的公差
的公差![]() 为已知常数,是否存在这样的实数p使得(1)中无穷等比数列
为已知常数,是否存在这样的实数p使得(1)中无穷等比数列![]() 各项的和
各项的和![]() ?并请说明理由.
?并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
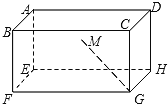
【题目】如图所示,在长方体![]() 中,AD=2,AB=AE=1,M为矩形AEHD内的一点,如果∠MGF=∠MGH,MG和平面EFG所成角的正切值为
中,AD=2,AB=AE=1,M为矩形AEHD内的一点,如果∠MGF=∠MGH,MG和平面EFG所成角的正切值为![]() 那么点M到平面EFGH的距离是_____.
那么点M到平面EFGH的距离是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,在同一个坐标系中,
,在同一个坐标系中,![]() 及
及![]() 的部分图象如图所示,则( ).
的部分图象如图所示,则( ).

A. 当![]() 时,
时,![]() 取得最大值 B. 当
取得最大值 B. 当![]() 时,
时,![]() 取得最大值
取得最大值
C. 当![]() 时,
时,![]() 取得最小值 D. 当
取得最小值 D. 当![]() 时,
时,![]() 取得最小值
取得最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个国际象棋棋盘(由8×8个方格组成),其中有一个小方格因破损而被剪去(破损位置不确定).“L”形骨牌由三个相邻的小方格组成,如图所示.现要将这个破损的棋盘剪成数个“L”形骨牌,则( )
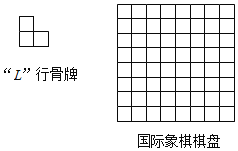
A.至多能剪成19块“L”形骨牌
B.至多能剪成20块“L”形骨牌
C.最多能剪成21块“L”形骨牌
D.前三个答案都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)的一种,现有十二生肖的吉物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学选取的礼物都满意,那么不同的选法有( )
A. 50种B. 60种C. 70种D. 90种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com