
【题目】某兴趣小组有男生20人,女生10人,从中抽取一个容量为5的样本,恰好抽到2名男生和3名女生,则
①该抽样可能是系统抽样;
②该抽样可能是随机抽样:
③该抽样一定不是分层抽样;
④本次抽样中每个人被抽到的概率都是![]() .
.
其中说法正确的为( )
A.①②③B.②③C.②③④D.③④
【答案】A
【解析】
①该抽样可以是系统抽样;②因为总体个数不多,容易对每个个体进行编号,因此该抽样可能是简单的随机抽样;③若总体由差异明显的几部分组成时,经常采用分层抽样的方法进行抽样,且分层抽样的比例相同,该抽样不可能是分层抽样;④分别求出男生和女生的概率,故可判断出真假.
①总体容量为30,样本容量为5,第一步对30个个体进行编号,如男生1~20,女生21~30;
第二步确定分段间隔![]() ;第三步在第一段用简单随机抽样确定第一个个体编号
;第三步在第一段用简单随机抽样确定第一个个体编号![]() ;
;
第四步将编号为![]() 依次抽取,即可获得整个样本.故该抽样可以是系统抽样.因此①正确.
依次抽取,即可获得整个样本.故该抽样可以是系统抽样.因此①正确.
②因为总体个数不多,可以对每个个体进行编号,因此该抽样可能是简单的随机抽样,故②正确;
③若总体由差异明显的几部分组成时,经常采用分层抽样的方法进行抽样,且分层抽样的比例相同,
但兴趣小组有男生20人,女生10人,抽取2男3女,抽的比例不同,故③正确;
④该抽样男生被抽到的概率![]() ;女生被抽到的概率
;女生被抽到的概率![]() ,故前者小于后者.因此④不正确.
,故前者小于后者.因此④不正确.
故选:A.


科目:高中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)设数列![]() 满足
满足![]() ,前
,前![]() 项和为
项和为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:
(1)由题意结合三角形内角和为![]() 可得
可得![]() .由余弦定理可得
.由余弦定理可得![]() ,,结合勾股定理可知
,,结合勾股定理可知![]() 为直角三角形,
为直角三角形,![]() ,
,![]() .
.
(2)结合(1)中的结论可得![]()
![]() .则
.则![]()
![]() ,
,![]() 据此可得关于实数k的方程
据此可得关于实数k的方程![]() ,解方程可得
,解方程可得![]() ,则
,则![]() 或
或![]() .
.
试题解析:
(1)由已知![]() ,又
,又![]() ,所以
,所以![]() .又由
.又由![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() 为直角三角形,
为直角三角形,![]() ,
,![]() .
.
(2)![]()
![]() .
.
所以![]()
![]()
![]() ,
,![]() 由
由![]() ,得
,得
![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 或
或![]() .
.
【题型】解答题
【结束】
18
【题目】已知点![]() 是平行四边形
是平行四边形![]() 所在平面外一点,如果
所在平面外一点,如果![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高二年级学生中,对自然科学类、社会科学类校本选修课程的选课意向进行调查.现从高二年级学生中随机抽取180名学生,其中男生105名;在这180名学生中选择社会科学类的男生、女生均为45名.
(1)根据抽取的180名学生的调查结果,完成下面的2×2列联表.
(2)判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考公式:![]() ,其中
,其中![]() .
.
P(K2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 | |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 和椭圆
和椭圆![]() . 直线
. 直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
(Ⅰ) 求椭圆![]() 的离心率;
的离心率;
(Ⅱ) 当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅲ)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,当
,当![]() 为
为![]() 中点时,求
中点时,求![]() 的值 .
的值 .
查看答案和解析>>
科目:高中数学 来源: 题型:
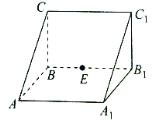
【题目】如图,三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,外接球的球心为
,外接球的球心为![]() ,点
,点![]() 是侧棱
是侧棱![]() 上的一个动点.有下列判断:①直线
上的一个动点.有下列判断:①直线![]() 与直线
与直线![]() 是异面直线;②
是异面直线;②![]() 一定不垂直于
一定不垂直于![]() ; ③三棱锥
; ③三棱锥![]() 的体积为定值;④
的体积为定值;④![]() 的最小值为
的最小值为![]() .其中正确的序号是______.
.其中正确的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
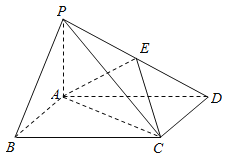
(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
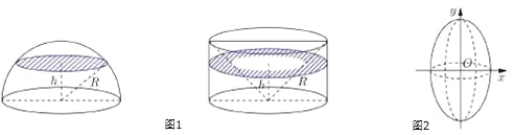
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com