Question

8．在△ABC中，点P为BC边上一点，且$\overrightarrow{BP}$=2$\overrightarrow{PC}$，$\overrightarrow{AP}=\frac{1}{3}\overrightarrow{AB}+λ\overrightarrow{AC}$，则λ=（　　）

• A． $-\frac{2}{3}$
• B． $-\frac{1}{3}$
• C． $\frac{1}{3}$
• D． $\frac{2}{3}$

Answer 1

分析 根据题意画出图形，结合图形利用平面向量的线性运算，即可得出λ的值．

解答 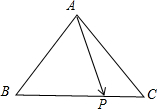解：如图所示，
△ABC中，$\overrightarrow{BP}$=2$\overrightarrow{PC}$，
∴$\overrightarrow{BP}$=$\frac{2}{3}$$\overrightarrow{BC}$=$\frac{2}{3}$（$\overrightarrow{AC}$-$\overrightarrow{AB}$）；
∴$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$=$\overrightarrow{AB}$+$\frac{2}{3}$（$\overrightarrow{AC}$-$\overrightarrow{AB}$）=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$，
又$\overrightarrow{AP}=\frac{1}{3}\overrightarrow{AB}+λ\overrightarrow{AC}$，
∴λ=$\frac{2}{3}$．
故选：D．

点评 本题主要考查了向量的加减运算问题，也考查了平面向量基本定理的应用问题，是容易题．