
| A. | ${\vec e_1}=(1,1)$与${\vec e_2}=(2,0)$ | B. | ${\vec e_1}=(1,1)$与${\vec e_2}=(2,2)$ | ||
| C. | ${\vec e_1}=(1,2)$与${\vec e_2}=(4,8)$ | D. | ${\vec e_1}=(-1,2)$与${\vec e_2}=(1,-2)$ |
分析 根据两个向量不是共线向量,即可判断它们能作为一组基底.
解答 解:对于A,$\overrightarrow{{e}_{1}}$=(1,1),与$\overrightarrow{{e}_{2}}$=(2,0)是不共线的向量,能作为一组基底;
对于B,因为$\overrightarrow{{e}_{1}}$=(1,1),$\overrightarrow{{e}_{2}}$=(2,2),满足$\overrightarrow{{e}_{1}}$=$\frac{1}{2}$$\overrightarrow{{e}_{2}}$,是共线向量,所以不能作为一组基底;
对于C,因为$\overrightarrow{{e}_{1}}$=(1,2),$\overrightarrow{{e}_{2}}$=(4,8),满足$\overrightarrow{{e}_{1}}$=$\frac{1}{4}$$\overrightarrow{{e}_{2}}$,是共线向量,所以不能作为一组基底;
对于D,因为$\overrightarrow{{e}_{1}}$=(-1,2),$\overrightarrow{{e}_{2}}$=(1,-2),满足$\overrightarrow{{e}_{1}}$=-$\overrightarrow{{e}_{2}}$,是共线向量,所以不能作为一组基底.
故选:A.
点评 本题考查了判断两个向量是否为共线向量的问题,是基础题目.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
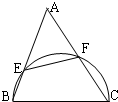 如图,△ABC中,BC=6,以BC为直径的半圆分别交AB,AC于点E,F,若AC=2AE.
如图,△ABC中,BC=6,以BC为直径的半圆分别交AB,AC于点E,F,若AC=2AE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知电流I与时间t的关系式为I=Asin(ωt+φ).
已知电流I与时间t的关系式为I=Asin(ωt+φ).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=($\root{3}{x}$)3和y=x | B. | y=($\sqrt{x}$)2和y=x | C. | y=$\sqrt{x^2}$和y=($\sqrt{x}$)2 | D. | y=$\root{3}{x^3}$和y=$\frac{x^2}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com