
选修4-4:坐标系与参数方程
已知曲线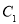 的参数方程为
的参数方程为 (
(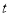 为参数),当
为参数),当 时,曲线
时,曲线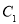 上对应的点为
上对应的点为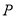 ,以原点
,以原点 为极
为极
点,以 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
(1)求证:曲线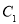 的极坐标方程为
的极坐标方程为 ;
;
(2)设曲线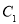 与曲线
与曲线 的公共点为
的公共点为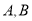 ,求
,求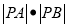 的值.
的值.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源:2016届广东省深圳市高三第二次调研考试数学(理)试卷(解析版) 题型:解答题
已知函数 ,直线
,直线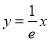 为曲线
为曲线 的切线(
的切线( 为自然对数的底数).
为自然对数的底数).
(1)求实数 的值;
的值;
(2)用 表示
表示 中的最小值,设函数
中的最小值,设函数 ,若函数
,若函数
 为增函数,求实数
为增函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届河南省高三下第二次联考文科数学卷(解析版) 题型:选择题
已知函数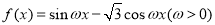 的图象的相邻两对称轴间的距离为
的图象的相邻两对称轴间的距离为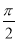 ,则当
,则当
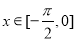 时,
时, 的最大值和单调区间分别为( )
的最大值和单调区间分别为( )
A.1,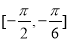 B.1,
B.1, C.
C.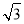 ,
,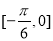 D.
D.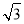 ,
,
查看答案和解析>>
科目:高中数学 来源:2016届河南省高三下第二次联考文科数学卷(解析版) 题型:选择题
下列命题中正确的是( )
A.若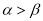 ,则
,则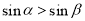 ;
;
B.命题:“ ”的否定是“
”的否定是“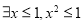 ”
”
C.直线 与
与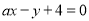 垂直的充要条件为
垂直的充要条件为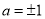 ;
;
D.“若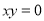 ,则
,则 或
或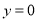 ”的逆否命题为“若
”的逆否命题为“若 或
或 ,则
,则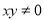 ”
”
查看答案和解析>>
科目:高中数学 来源:2016届河南省高三下第二次联考理科数学卷(解析版) 题型:解答题
某市于今年1月1日起实施小汽车限购政策,根据规定,每年发放10万个小汽车购买名额,其中电动小汽车占20%,通过摇号方式发放,其余名额通过摇号和竞价两种方式各发放一半,政策推出后,某网站针对不同年龄段的申请意向进行了调查,结果如下表所示.
申请意向年龄 | 摇号 | 竞价(人数) | 合计 | |
电动小汽车(人数) | 非电动小汽车(人数) | |||
30岁以下(含30岁) | 50 | 100 | 50 | 200 |
30至50岁(含50岁) | 50 | 150 | 300 | 500 |
50岁以上 | 100 | 150 | 50 | 300 |
合计 | 200 | 400 | 400 | 1000 |
(1)采取分层抽样的方式从30至50岁的人中抽取10人,求其中各种意向人数;
(2)在(1)中选出的10个人中随机抽取4人,求其中恰有2人有竞价申请意向的概率;
(3)用样本估计总体,在全体市民中任意选取4人,其中摇号申请电动小汽车意向的人数记为 ,求
,求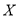
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2016届河南省洛阳市高三毕业班三练数学(文)试卷(解析版) 题型:
经销商经销某种产品,在一个销售周期内,每售出1件产品获得利润500元,未售出的产品每件亏损100元,根据过去的市场记录,得到了60个销售周期的市场需求量的频率分布表:

经销商为了下一个销售周期购进了130件产品,以 表示下一个销售周期内的市场需求量,
表示下一个销售周期内的市场需求量,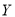 表示下一个销售周期内的经销产品的利润.
表示下一个销售周期内的经销产品的利润.
(1)画出市场需求量的频率分布直方图,并以各组的区间中点值代表该组的各个需求量,估计一个销售周期内的市场需求量的平均数;
(2)根据市场需求量的频率分布表提供的数据,估计下一个销售周期内的经销产品的利润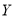 不少于53000元的概率.
不少于53000元的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com