Question

11．已知圆O_n：x²+y²=$\frac{1}{{n}^{2}}$（n∈N^*）与圆C：（x-1）²+y²=1，设圆O_n与y轴正半轴的交点为R_n，圆O_n与圆C在x轴上方的交点为O_n，直线R_nO_n交x轴于点P_n．当n趋向于无穷大时，点P_n无限趋近于定点P，定点P的横坐标为4．

Answer 1

分析 由题意求出R_n，O_n的坐标，求出直线R_nO_n的方程，进一步求出直线与x轴的交点坐标，取极限得答案．

解答 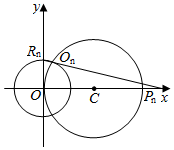解：如图，
∵圆O_n与y轴正半轴的交点为R_n，则${R}_{n}（0，\frac{1}{n}）$，
又圆O_n与圆C在x轴上方的交点为O_n，
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=\frac{1}{{n}^{2}}}\\{（x-1）^{2}+{y}^{2}=1}\end{array}\right.$，解得${O}_{n}（\frac{1}{2{n}^{2}}，\frac{\sqrt{4{n}^{2}-1}}{2{n}^{2}}）$，
∴${k}_{{R}_{n}{O}_{n}}$=$\frac{\frac{\sqrt{4{n}^{2}-1}}{2{n}^{2}}-\frac{1}{n}}{\frac{1}{2{n}^{2}}}$=$\sqrt{4{n}^{2}-1}-2n$，
则直线R_nO_n的方程为$y=（\sqrt{4{n}^{2}-1}-2n）x+\frac{1}{n}$，
取y=0，得$x=-\frac{1}{n（\sqrt{4{n}^{2}-1}-2n）}$=$\frac{2n+\sqrt{4{n}^{2}-1}}{n}$．
当n→∞时，x→4，
∴定点P的横坐标为4．
故答案为：4．

点评 本题考查圆与圆位置关系的判定，考查了直线方程的求法，训练了极限思想方法的运用，是中档题．