
分析 由抛物线方程,求导,利用导数的几何意义,求得P点的切线方程的斜率,求得切线方程,当x=-1时,求得N点坐标,由$\overrightarrow{PF}$=(1-x0,-y0),$\overrightarrow{FN}$=(-2,$\frac{2({x}_{0}-1)}{{y}_{0}}$),则$\overrightarrow{PF}$•$\overrightarrow{FN}$=0,$\overrightarrow{PF}$⊥$\overrightarrow{FN}$,由丨PQ丨=丨QF丨,则△NPQ≌△NPF,即可求得∠PNQ=∠PNF,即可求得∠PNF=∠NMF,即可求得MF=NF,则$\frac{MF}{NF}$=1,
解答 解:抛物线C:y2=4x的焦点为F(1,0),准线为l:x=-1,
抛物线y2=4x两边对x求导,可得2yy′=4,即y′=$\frac{2}{y}$,
过P(x0,y0)(y0≠0)的切线为l的斜率为$\frac{2}{{y}_{0}}$,切线的方程为y-y0=$\frac{2}{{y}_{0}}$(x-x0),
又y02=4x0,即有y0y=2(x+x0),
令x=-1,可得N(-1,$\frac{2({x}_{0}-1)}{{y}_{0}}$),
∴$\overrightarrow{PF}$=(1-x0,-y0),$\overrightarrow{FN}$=(-2,$\frac{2({x}_{0}-1)}{{y}_{0}}$),
∴$\overrightarrow{PF}$•$\overrightarrow{FN}$=-2(1-x0)-y0•$\frac{2({x}_{0}-1)}{{y}_{0}}$=0,
∴$\overrightarrow{PF}$⊥$\overrightarrow{FN}$,
过P做PQ垂直于x=-1,交x=-1于Q,
由椭圆的定义可知:丨PQ丨=丨QF丨,
∴△NPQ≌△NPF,
∴∠PNQ=∠PNF,
∵∠PNQ=∠NMF,
∴∠PNF=∠NMF,
∴MF=NF,
$\frac{MF}{NF}$=1,
故答案为:1.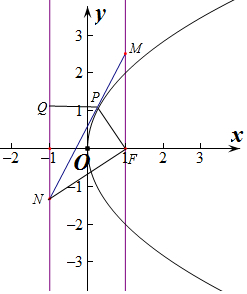
点评 本题考查导数的几何意义,向量数量积的坐标表示,直线垂直的充要条件,抛物线的性质及相似三角形的性质的综合利用,考查数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4+2$\sqrt{3}$ | C. | 4+2$\sqrt{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (17,25) | B. | (9,25) | C. | (8,25) | D. | (9,17) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com