
| A. | 2 | B. | 12 | C. | 4 | D. | 6 |
分析 由向量加法的三角形法则得$\overrightarrow{CM}$=$\frac{2}{3}$$\overrightarrow{CA}$+$\frac{1}{3}$$\overrightarrow{CB}$,然后利用向量数量积运算性质可求答案.
解答 解:$\overrightarrow{CM}$=$\overrightarrow{CB}$+$\frac{2}{3}$$\overrightarrow{BA}$=$\overrightarrow{CB}$+$\frac{2}{3}$($\overrightarrow{CA}$-$\overrightarrow{CB}$)=$\frac{2}{3}$$\overrightarrow{CA}$+$\frac{1}{3}$$\overrightarrow{CB}$,
∴$\overrightarrow{CM}$•$\overrightarrow{CB}$=($\frac{2}{3}$$\overrightarrow{CA}$+$\frac{1}{3}$$\overrightarrow{CB}$)•$\overrightarrow{CB}$=+$\frac{2}{3}$•$\overrightarrow{CA}$•$\overrightarrow{CB}$+$\frac{1}{3}$${\overrightarrow{CB}}^{2}$=$\frac{1}{3}$×62=12,
故选:B
点评 本题考查平面向量的运算性质、向量加法的三角形法则,属基础题


科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | $\frac{24}{25}$ | C. | -$\frac{7}{25}$ | D. | -$\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
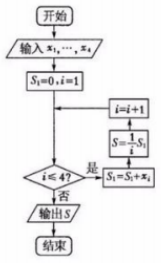 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为xi(i=1,2,3,4)(单位:立方米).根据如图所示的程序框图,若知x1,x2,x3,x4分别为1,1.5,1.5,3,则输出的结果S为$\frac{7}{4}$.
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为xi(i=1,2,3,4)(单位:立方米).根据如图所示的程序框图,若知x1,x2,x3,x4分别为1,1.5,1.5,3,则输出的结果S为$\frac{7}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$或$\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$或$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com