
分析 (Ⅰ)对函数f(x)求导,再根据导数和函数极值的关系分类即可得到极值点的个数,
(Ⅱ)命题“?x∈[0,+∞),f(x)≥kg(x)”是假命题,转化为不等式f(x)<kg(x)在区间[0,+∞)内有解,再构造函数F(x)=f(x)-kg(x)ex+kln(x+1)-(k+1)x-1,利用导数和函数的单调性关系以及函数零点存在定理判断即可.
解答 解:(Ⅰ)因为f(x)=aex-x-1,所以f'(x)=aex-1,
当a≤0时,对?x∈R,f'(x)=aex-1<0,
所以f(x)在(-∞,+∞)是减函数,此时函数不存在极值,
所以函数f(x)没有极值点;
当a>0时,f'(x)=aex-1,令f'(x)=0,解得x=-lna,
若x∈(-∞,-lna),则f'(x)<0,所以f(x)在(-∞,-lna)上是减函数,
若x∈(-lna,+∞),则f'(x)>0,所以f(x)在(-lna,+∞)上是增函数,
当x=-lna时,f(x)取得极小值为f(-lna)=lna,
函数f(x)有且仅有一个极小值点x=-lna,
所以当a≤0时,f(x)没有极值点,当a>0时,f(x)有一个极小值点.
(Ⅱ)命题“?x∈[0,+∞),f(x)≥kg(x)”是假命题,
则“?x∈[0,+∞),f(x)<kg(x)”是真命题,
即不等式f(x)<kg(x)在区间[0,+∞)内有解.
若a=1,则设F(x)=f(x)-kg(x)=ex+kln(x+1)-(k+1)x-1,
所以$F'(x)={e^x}+\frac{k}{x+1}$-(k+1),
设$h(x)={e^x}+\frac{k}{x+1}$-(k+1),
则$h'(x)={e^x}-\frac{k}{{{{({x+1})}^2}}}$,且h'(x)是增函数,
所以h'(x)≥h'(0)=1-k
当k≤1时,h'(x)≥0,
所以h(x)在[0,+∞)上是增函数,h(x)≥h(0)=0,即F'(x)≥0,
所以F(x)在[0,+∞)上是增函数,
所以F(x)≥F(0)=0,即f(x)≥kg(x)在x∈[0,+∞)上恒成立.
当k>1时,因为$h'(x)={e^x}-\frac{k}{{{{({x+1})}^2}}}$在[0,+∞)是增函数,
因为h'(0)=1-k<0,h'(k-1)=${e^{k-1}}-\frac{1}{k}>0$,
所以h'(x)在(0,k-1)上存在唯一零点x0,
当x∈[0,x0)时,h'(x)<h'(x0)=0,h(x)在[0,x0)上单调递减,
从而h(x)≤h(0)=0,即F'(x)≤0,所以F(x)在[0,x0)上单调递减,
所以当x∈(0,x0)时,F(x)<F(0)=0,即f(x)<kg(x).
所以不等式f(x)<kg(x)在区间[0,+∞)内有解
综上所述,实数k的取值范围为(1,+∞).
点评 本题考查了导数的综合应用及恒成立问题的处理方法,同时考查了分类讨论的思想及单调性的判断与应用,化简及分类讨论比较困难,属于难题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{1}{6},5}]$ | B. | [1,5] | C. | $[{\frac{1}{4},5}]$ | D. | [0,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 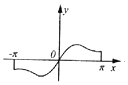 | C. | 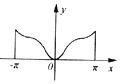 | D. | 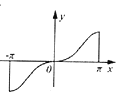 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2017}{2018}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2016}{2017}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com