练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．直线l与圆x2+y2+2x-4y+a=0（a＜3）交于A，B两点，且弦AB的中点为（0，1），则直线l的方程是（　　）
    A．y=-2x+1B．y=2x+1C．y=-x+1D．y=x+1

    分析 求出圆心的坐标，再求出弦中点与圆心连线的斜率，然后再求出弦所在直线的斜率，由点斜式即可写出直线方程．

    解答 解：由题意，圆心为O（-1，2），
    设直线l的斜率为k，弦AB的中点为P（0，1），PO的斜率为kop，
    则kOP=$\frac{2-1}{-1-0}$=-1；
    又l⊥PO，∴k•kop=k•（-1）=-1，解得k=1；
    由点斜式得直线l的方程为：y=x+1．
    故选：D．

    点评 考查求直线的方程，本题已知弦中点的坐标，再根据弦与弦心距对应直线垂直求斜率k．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

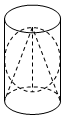    20．利用浮力原理巧妙地称出了皇冠中黄金的重量的阿基米德，在他的墓碑上有一幅几何图案，如图所示，因为阿基米德很欣赏这三者的体积之比为V圆锥：V球：V圆柱=1：2：3，他还得出球的表面积与它的外切圆柱的表面积之比等于它们的体积之比，都等于2：3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．函数f（x）=2x3+3x2-12x的极小值是-7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知α，β是两个不同的平面，m，n是两条不同的直线，给出下列命题：
    ①若m⊥α，m?β，则α⊥β；
    ②若m⊥n，m⊥α，则n∥α；
    ③若α∩β=m，n∥m，且n?α，n?β，则n∥α且n∥β．
    ④若m∥α，α⊥β，则m⊥β．
    其中真命题的个数是2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知a，b为实数．
    （Ⅰ）若a＞0，b＞0，求证：（a+b+$\frac{1}{a}$）（a2+$\frac{1}{b}$+$\frac{1}{{a}^{2}}$）≥9；
    （Ⅱ）若|a|＜1，|b|＜1，求证：|1-ab|＞|a-b|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．i是虚数单位，若$\frac{2+i}{1+i}$=a+bi（a，b∈R），则log2（a-b）的值是（　　）
    A．-1B．1C．0D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．设等比数列{an}的前n项和为Sn，若S12：S6=1：2，则S18：S63：4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知i为虚数单位，则复数$\frac{{1-\frac{1}{2}i}}{{1+\frac{1}{2}i}}$在复平面所对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若函数y=f（x）在定义域内给定区间[a，b]上存在x0（a＜x0＜b），满足f（x0）=$\frac{f（b）-f（a）}{b-a}$，则称函数y=f（x）是[a，b]上的“平均值函数”，x0是它的一个均值点．例如y=|x|是[-2，2]上的“平均值函数”，0是它的均值点．若f（x）=lnx是区间[a，b]（b＞a≥1）上的“平均值函数”，x0是它的一个均值点，则lnx0与$\frac{1}{{\sqrt{ab}}}$的大小关系是（　　）
    A．lnx0=$\frac{1}{{\sqrt{ab}}}$B．lnx0≤$\frac{1}{{\sqrt{ab}}}$C．lnx0≥$\frac{1}{{\sqrt{ab}}}$D．lnx0＜$\frac{1}{{\sqrt{ab}}}$

    查看答案和解析>>

    同步练习册答案