
分析 ①根据面面垂直的判定定理进行判断即可,
②根据线面平行的性质以及线面垂直的性质进行判断,
③根据线面平行的判定定理进行判断,
④根据线面平行,面面垂直的判定定理进行判断.
解答 解:①根据面面垂直的定义知若一个平面内有一条直线和平面垂直,则两个平面垂直,即若m⊥α,m?β,则α⊥β成立;故①正确,
②若m⊥n,m⊥α,则n∥α或n?α;故②错误,
③若α∩β=m,n∥m且n?α,n?β,则n∥α且n∥β此命题正确,因为由线面平行的判定定理知,面外一条直线与面内一条直线平行,可得此线与面平行.故③正确,
④若m∥α,α⊥β,则m⊥β或m∥β或m?β或m与β相交.故④错误,
故正确的是①③,
故答案为:2
点评 本题主要考查命题的真假判断,涉及空间直线和平面,平面和平面平行或垂直的判定,根据相应的判定定理和性质定理是解决本题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{2},1)$ | B. | (0,1) | C. | $(0,\frac{1}{2}]$ | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-2x+1 | B. | y=2x+1 | C. | y=-x+1 | D. | y=x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
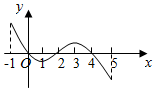 已知函数f(x)的定义域为[-1,5],部分对应值如表,y=f'(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如表,y=f'(x)的图象如图所示,下列关于函数f(x)的命题:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$i | C. | $\frac{\sqrt{5}}{5}$ | D. | -i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com