
【题目】已知椭圆![]()
![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点相同,
的焦点相同, ![]() 为椭圆的左、右焦点.
为椭圆的左、右焦点. ![]() 为椭圆上任意一点,
为椭圆上任意一点, ![]() 面积的最大值为1.
面积的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点.若直线
两点.若直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() .求证:直线
.求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】设离心率为 ![]() 的椭圆E:
的椭圆E: ![]() +
+ ![]() =1(a>b>0)的左、右焦点为F1 , F2 , 点P是E上一点,PF1⊥PF2 , △PF1F2内切圆的半径为
=1(a>b>0)的左、右焦点为F1 , F2 , 点P是E上一点,PF1⊥PF2 , △PF1F2内切圆的半径为 ![]() ﹣1.
﹣1.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线y=x+2,A、B在椭圆E上,若矩形ABCD的周长为 ![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,椭圆
轴上,椭圆![]() 上的点到焦点距离的最大值为3,最小值为1.
上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点(
两点(![]() ,
, ![]() 不是左右顶点),且以
不是左右顶点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的右顶点.求证:直线
的右顶点.求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全国大学生机器人大赛是由共青团中央,全国学联,深圳市人民政府联合主办的赛事,是中国最具影响力的机器人项目,是全球独创的机器人竞技平台.全国大学生机器人大赛比拼的是参赛选手们的能力,坚持和态度,展现的是个人实力以及整个团队的力量.2015赛季共吸引全国240余支机器人战队踊跃报名,这些参赛战队来自全国六大赛区,150余所高等院校,其中不乏北京大学,清华大学,上海交大,中国科大,西安交大等众多国内顶尖高校,经过严格筛选,最终由111支机器人战队参与到2015年全国大学生机器人大赛的激烈角逐之中,某大学共有“机器人”兴趣团队1000个,大一、大二、大三、大四分别有100,200,300,400个,为挑选优秀团队,现用分层抽样的方法,从以上团队中抽取20个团队.
(1)应从大三抽取多少个团队?
(2)将20个团队分为甲、乙两组,每组10个团队,进行理论和实践操作考试(共150分),甲、乙两组的分数如下:
甲:125,141,140,137,122,114,119,139,121,142
乙:127,116,144,127,144,116,140,140,116,140
从甲、乙两组中选一组强化训练,备战机器人大赛.从统计学数据看,若选择甲组,理由是什么?若选择乙组,理由是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .

(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线x2=ay(a>0)的准线l与y轴交于点P,若l绕点P以每秒 ![]() 弧度的角速度按逆时针方向旋转t秒钟后,恰与抛物线第一次相切,则t等于( )
弧度的角速度按逆时针方向旋转t秒钟后,恰与抛物线第一次相切,则t等于( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M到坐标原点的距离和它到直线l:x=﹣m(m>0)的距离之比是一个常数 ![]() .
.
(Ⅰ)求点M的轨迹;
(Ⅱ)若m=1时得到的曲线是C,将曲线C向左平移一个单位长度后得到曲线E,过点P(﹣2,0)的直线l1与曲线E交于不同的两点A(x1 , y1),B(x2 , y2),过F(1,0)的直线AF、BF分别交曲线E于点D、Q,设 ![]() =α
=α ![]() ,
, ![]() =β
=β ![]() ,α、β∈R,求α+β的取值范围.
,α、β∈R,求α+β的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 在区间
在区间![]() 上的图像如图所示,将该函数图像上各点的横坐标缩短到原来的一半(纵坐标不变),再向右平移
上的图像如图所示,将该函数图像上各点的横坐标缩短到原来的一半(纵坐标不变),再向右平移![]() 个单位长度后,所得到的图像关于直线
个单位长度后,所得到的图像关于直线![]() 对称,则
对称,则![]() 的最小值为( )
的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点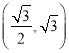 ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆的上顶点作直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,
两点, ![]() 为原点.
为原点.
①求证: ![]() ;
;
②设![]() 、
、![]() 分别与椭圆相交于
分别与椭圆相交于![]() 、
、![]() 两点,过原点
两点,过原点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com