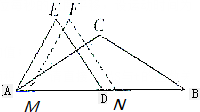
如图,等腰△ABC和等边△ADE的顶点A、D、B在同一条直线上,AC=BC=12,点D是AB的中点,∠ACB=120°,△MNF与△ADE完全重合,将△MNF从△ADE处沿AB方向以
个单位每秒的速度平移,设运动时间为t秒(t>0),当点M到达点B时停止运动.
(1)在整个平移过程中,求出NF、MF分别过点C时t的值;
(2)在整个平移过程中,△MNF与△ABC重叠部分的面积为S,请直接写出S与t的函数关系式,以及相应的自变量t的取值范围;
(3)当停止运动时,将△MNF绕点N沿顺时针方向旋转,设旋转角为α,0°<α<180°.在旋转过程中,MN与AC、AE交于点G、点H.以点A、G、H为顶点的三角形能否是等腰三角形,若是,请求出AG的长,若不是,请说明理由.