
| A. | 36种 | B. | 30种 | C. | 24种 | D. | 20种 |
分析 根据题意中甲要求不到A学校,分析可得对甲有2种不同的分配方法,进而对剩余的三人分情况讨论,①其中有一个人与甲在同一个学校,②没有人与甲在同一个学校,易得其情况数目,最后由分步计数原理计算可得答案.
解答 解:根据题意,首先分配甲,有2种方法,
再分配其余的三人:分两种情况,①其中有一个人与甲在同一个学校,有A33=6种情况,
②没有人与甲在同一个学校,则有C32•A22=6种情况;
则若甲要求不到A学校,则不同的分配方案有2×(6+6)=24种;
故选:C.
点评 本题考查排列、组合的综合运用,注意题意中“每个学校至少分配一人”这一条件,再分配甲之后,需要对其余的三人分情况讨论.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
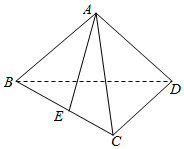 如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.
如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com