
分析 (1)化圆的一般方程为标准方程,求出圆心坐标和半径,利用垂径定理求得c值;
(2)化直线方程为一般式,求出圆心到直线的距离,减去半径得答案.
解答 解:(1)由x2+y2-2x+4y-20=0,得(x-1)2+(y+2)2=52,
∴圆心坐标为(1,-2),半径r=5,
∵圆x2+y2-2x+4y-20=0截直线5x-12y+c=0的弦长为8,
∴圆心到直线5x-12y+c=0的距离为3,即$\frac{|5+24+c|}{13}=3$,解得:c=10或c=-68;
(2)由y=x-11,得x-y-11=0,
圆心(1,-2)到直线的距离d=$\frac{|1+2-11|}{\sqrt{2}}=4\sqrt{2}$,
∴直线y=x-11上的点到圆上点的最短距离为$4\sqrt{2}-5$.
点评 本题考查直线与原点位置关系,考查了点到直线距离公式的应用,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
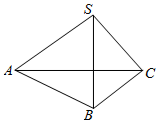 如图,在四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,求:
如图,在四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 30种 | C. | 24种 | D. | 20种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校高三期中考试后,数学教师对本次全部数学成绩按 1:20进行分层抽样,随机抽取了 20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如下表所示的频率分布表:
某校高三期中考试后,数学教师对本次全部数学成绩按 1:20进行分层抽样,随机抽取了 20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如下表所示的频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150] | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}+\frac{2}{5}i$ | B. | $\frac{1}{5}+\frac{2}{5}i$ | C. | $-\frac{1}{5}-\frac{2}{5}i$ | D. | $\frac{1}{5}-\frac{2}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com