
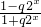 .
. ,函数g(x)在[0,1]上的上界是H(q),求H(q)的取值范围;
,函数g(x)在[0,1]上的上界是H(q),求H(q)的取值范围; )x+(
)x+( )x,
)x,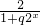 -1,∵q>0,x∈[0,1],∴g(x)在[0,1]上递减,
-1,∵q>0,x∈[0,1],∴g(x)在[0,1]上递减,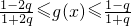 ,
, ],∴|
],∴|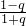 |≥|
|≥|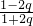 |,
|,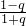 |,
|,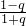 |,即H(q)的取值范围为[|
|,即H(q)的取值范围为[|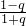 |,+∞).
|,+∞). )x,t∈(0,1],由-3≤f(x)≤3,得-3≤1+pt+t2≤3,
)x,t∈(0,1],由-3≤f(x)≤3,得-3≤1+pt+t2≤3, )≤p≤
)≤p≤ -t在(0,1]上恒成立,
-t在(0,1]上恒成立, ,m(t)=
,m(t)= -t,则h(t)在(0,1]上递增;m(t)在(0,1]上递减,
-t,则h(t)在(0,1]上递增;m(t)在(0,1]上递减, )x+(
)x+(  )x,可判断f(x)在(-∞,0)上的单调性,由单调性可得求得f(x)在(-∞,0)上的值域,由值域可判断函数f(x)在(-∞,0)上是否为有界函数.
)x,可判断f(x)在(-∞,0)上的单调性,由单调性可得求得f(x)在(-∞,0)上的值域,由值域可判断函数f(x)在(-∞,0)上是否为有界函数. 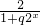 -1,易判断g(x)在[0,1]上的单调性,由单调性可求得g(x)的值域,进而求得|g(x)|的值域,由上界定义可求得H(q)的范围;
-1,易判断g(x)在[0,1]上的单调性,由单调性可求得g(x)的值域,进而求得|g(x)|的值域,由上界定义可求得H(q)的范围; )x,t∈(0,1],则转化为3≤1+pt+t2≤3恒成立,分离参数p后转化为求函数最值即可解决;
)x,t∈(0,1],则转化为3≤1+pt+t2≤3恒成立,分离参数p后转化为求函数最值即可解决;

科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1-m•x2 |
| 1+m•x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1-m•x2 |
| 1+m•x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| x2-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)| 48 |
| x |
| t+1 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com