
分析 根据几何体的特征,小圆的圆心为Q,若四面体ABCD的体积的最大值,由于底面积S△ABC不变,高最大时体积最大,可得DQ与面ABC垂直时体积最大,最大值为$\frac{1}{3}$S△ABC×DQ
解答  解:根据题意知,A、B、C三点均在球心O的表面上,且|AB|=|AC|=1,∠BAC=120°,
解:根据题意知,A、B、C三点均在球心O的表面上,且|AB|=|AC|=1,∠BAC=120°,
∴BC=$\sqrt{3}$,
∴△ABC外接圆半径2r=2,即r=1,
∴S△ABC=$\frac{1}{2}$×1×1×sin120°=$\frac{\sqrt{3}}{4}$,
小圆的圆心为Q,若四面体ABCD的体积的最大值,由于底面积S△ABC不变,高最大时体积最大,
所以,DQ与面ABC垂直时体积最大,最大值为$\frac{1}{3}$S△ABC×DQ,
在直角△AQO中,OA2=AQ2+OQ2,即22=12+OQ2,∴OQ=$\sqrt{3}$,
∴DQ=2+$\sqrt{3}$,
∴最大值为$\frac{1}{3}$S△ABC×DQ=$\frac{1}{3}•\frac{\sqrt{3}}{4}•$(2+$\sqrt{3}$)=$\frac{3+2\sqrt{3}}{12}$,
故答案为:$\frac{3+2\sqrt{3}}{12}$.
点评 本题考查的知识点是球内接多面体,球的表面积,其中分析出何时四面体ABCD的体积的最大值,是解答的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提与推理形式都错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
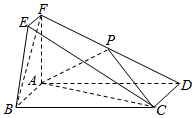 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P在棱DF上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
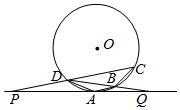 如图,四边形ABCD是⊙O的内接四边形,且AB∥CD,过点A作⊙O的切线,与CD,DB的延长线分别交于点P,Q.
如图,四边形ABCD是⊙O的内接四边形,且AB∥CD,过点A作⊙O的切线,与CD,DB的延长线分别交于点P,Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
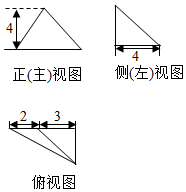 已知某几何体的三视图如图所示,则该几何体的体积是( )
已知某几何体的三视图如图所示,则该几何体的体积是( )| A. | 28+6$\sqrt{5}$ | B. | 40 | C. | $\frac{40}{3}$ | D. | 30+6$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
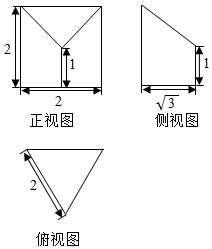 如图是某几何体的三视图,则该几何体体积是( )
如图是某几何体的三视图,则该几何体体积是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{5\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com