
分析 (I)求得函数f(x)的导数,由导数大于0,可得增区间;导数小于0,可得减区间;
(II)求出f(x)的导数f′(x),再求导数f''(x),讨论k的范围,①当2k≤4即k≤2时,②当2k>4即k>2时,求出导数符号,确定单调性,即可得到所求范围;
(Ⅲ)由(II)知,e2x≥1+2x+2x2,令x=1,2,…,n-1,可得n-1个不等式,累加,运用不等式的性质和求和公式,即可得到所求大小关系.
解答 解:(I)函数f(x)=e2x-1-2x的导数为f′(x)=2(e2x-1),
∵x>0时f′(x)>0,x<0时f′(x)<0,
∴单调递增区间为(0,+∞);单调递减区间为(-∞,0);
(II)f(x)的导数为f′(x)=2e2x-2-2kx,f''(x)=4e2x-2k,
①当2k≤4即k≤2时,f''(x)>0⇒f′(x)单调递增⇒f′(x)≥0⇒f(x)单调递增
⇒f(x)≥f(0)=0恒成立,∴k≤2使原式成立;
②当2k>4即k>2时,?x0>0使x∈[0,x0)时f''(x)<0⇒f′(x)单调递减
⇒f′(x)≤f′(0)=0⇒f(x)单调递减⇒f(x)<f(0)=0不满足条件.
综上可得,k≤2;
(Ⅲ)由(II)知,当k=2时,e2x-1-2x-kx2≥0成立,即e2x≥1+2x+2x2,
取x=n得e2n>1+2n+2n2,e2>1+2+2,e4>1+2×2+2×22,e6>1+2×3+2×32,
…e2(n-1)>1+2(n-1)+2(n-1)2,
∴$\frac{{{e^{2n}}-1}}{{{e^2}-1}}=1+{e^2}+{e^4}+…+{e^{2(n-1)}}$>n+2[1+2+3+…+(n-1)]+2[12+22+…+(n-1)2]
=$n+n(n-1)+\frac{n(n-1)(2n-1)}{3}=\frac{{2{n^3}+n}}{3}$.
所以$\frac{{{e^{2n}}-1}}{{{e^2}-1}}$≥$\frac{{2{n^3}}}{3}+\frac{n}{3}$(n=1时取等号).
点评 本题考查导数的运用:求单调区间,考查不等式恒成立问题的解法,注意运用分类讨论的思想方法,考查两式的大小比较,注意运用不等式的性质和累加法,考查化简整理的运算能力,属于中档题.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 试通过建立空间直角坐标系,利用空间向量解决下列问题:
试通过建立空间直角坐标系,利用空间向量解决下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
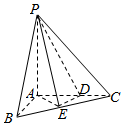 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=3,AB=$\frac{3}{2}$,BE=$\frac{1}{2}$EC,AD=2DC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=3,AB=$\frac{3}{2}$,BE=$\frac{1}{2}$EC,AD=2DC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD边长为2,以A为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连接BF并延长交CD于点E.
如图,正方形ABCD边长为2,以A为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连接BF并延长交CD于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
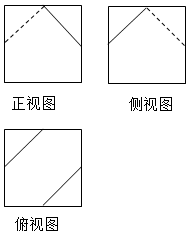 一个棱长为4的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为( )
一个棱长为4的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为( )| A. | 40 | B. | $\frac{136}{3}$ | C. | 56 | D. | $\frac{184}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com