
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,侧棱
是矩形,侧棱![]() 底面
底面![]() ,且
,且![]() ,
,![]() 为棱
为棱![]() 的中点,作
的中点,作![]() 交
交![]() 于点
于点![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() ,求
,求![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见详解;(2)![]() .
.
【解析】
(1)先证![]() ,结合已知条件,即可求证;
,结合已知条件,即可求证;
(2)建立空间直角坐标系,由二面角大小求得![]() 长度,再用线面角的定义即可求解.
长度,再用线面角的定义即可求解.
(1)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() ;
;
又因为四边形![]() 为矩形,故可得
为矩形,故可得![]() ;
;
又![]() 平面
平面![]() ,且
,且![]() ,
,
故可得![]() 平面
平面![]() ;
;
又因为![]() 平面
平面![]() ,故可得
,故可得![]() ,
,
又因为![]() ,
,![]() 为
为![]() 中点,故
中点,故![]() ,
,
结合![]() 平面
平面![]() ,
,![]() ,
,
故可得![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,则
,则![]() .
.
由题可知![]() ,又
,又![]() 平面
平面![]() ,
,![]() ,
,
即证![]() 平面
平面![]() .
.
(2)因为![]() 平面
平面![]() ,且底面
,且底面![]() 为矩形,
为矩形,
故可得![]() 两两垂直.
两两垂直.
则以![]() 为坐标原点,
为坐标原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
如下图所示:
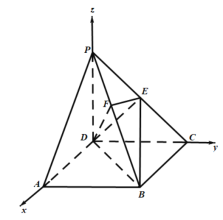
不妨设![]() ,故可得
,故可得
![]() ,
,
由(1)中所得可知![]() 为平面
为平面![]() 的法向量,
的法向量,
容易知![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
又因为面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() ,
,
故可得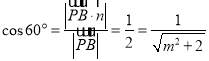 ,解得
,解得![]() .
.
又因为![]() 平面
平面![]() ,故可得
,故可得![]() 即为所求.
即为所求.
在![]() 中,
中,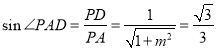 .
.
故![]() 与面
与面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】男运动员6名,女运动员4名,其中男女队长各1名.选派5人外出比赛,在下列情形中各有多少种选派方法?
(1)男运动员3名,女运动员2名;
(2)至少有1名女运动员;
(3)队长中至少有1人参加;
(4)既要有队长,又要有女运动员.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内的两点![]() 满足条件:①
满足条件:①![]() 都在函数
都在函数![]() 的图象上;②
的图象上;②![]() 关于原点对称.则称点对
关于原点对称.则称点对![]() 是函数
是函数![]() 的一对“友好点对”(点对
的一对“友好点对”(点对![]() 与
与![]() 看作同一对“友好点对”).已知函数
看作同一对“友好点对”).已知函数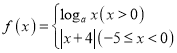 (
(![]() 且
且![]() ),若此函数的“友好点对”有且只有一对,则
),若此函数的“友好点对”有且只有一对,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某社团为调查大学生对于“中华诗词”的喜好,从甲、乙两所大学各随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:

根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级 :
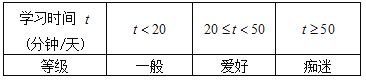
(Ⅰ)从甲大学中随机选出一名学生,试估计其“爱好”中华诗词的概率;
(Ⅱ)从两组“痴迷”的同学中随机选出2人,记![]() 为选出的两人中甲大学的人数,求
为选出的两人中甲大学的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(Ⅲ)试判断选出的这两组学生每天学习“中华诗词”时间的平均值![]() 与
与![]() 的大小,及方差
的大小,及方差![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节约资源和保护环境是中国的基本国策.某化工企业,积极响应国家要求,探索改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良后所排放的废气中含有的污染物数量为
,首次改良后所排放的废气中含有的污染物数量为![]() .设改良工艺前所排放的废气中含有的污染物数量为
.设改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良工艺后所排放的废气中含有的污染物数量为
,首次改良工艺后所排放的废气中含有的污染物数量为![]() ,则第n次改良后所排放的废气中的污染物数量
,则第n次改良后所排放的废气中的污染物数量![]() ,可由函数模型
,可由函数模型![]() 给出,其中n是指改良工艺的次数.
给出,其中n是指改良工艺的次数.
(1)试求改良后所排放的废气中含有的污染物数量的函数模型;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过![]() ,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.
,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.
(参考数据:取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,在
,在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,总有
怎样变化,总有![]() 为直角?若存在,求出点
为直角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com