
分析 (1)根据对任意x∈R,f(x+1)=f(x+2)+f(x)恒成立,以及递推关系可得f(x+3)=-f(x),将x+3代入可得f(x+6)=f(x),最后根据周期函数的定义可知f(x)的周期,从而证得结论;
(2)根据f(x)是周期函数且6是它的一个周期,将f(2010)转化成f(0),而f(0)与f(3)互为相反数,即可求出所求.
解答 (1)证明:由f(x+1)=f(x+2)+f(x),得f(x+2)=f(x+3)+f(x+1)
∴f(x+3)+f(x)=0,f(x+3)=-f(x)
因此f(x+6)=-f(x+3)=f(x).
∴f(x)是周期函数,且6是它的一个周期.
(2)∵f(x+3)=-f(x)且f(3)=-2,∴f(0)=-f(3)=2.
又f(2 010)=f(335×6)=f(0),∴f(2 010)=2.
点评 本题主要考查了抽象函数的周期性,以及求函数值等有关知识,同时考查了转化与化归的思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
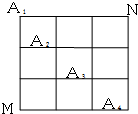 如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 随机数组的特征 | 3个数字均相同 | 恰有2个数字相同 | 其余情况 |
| 奖金(单位:元) | 500 | 200 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com