练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若椭圆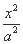+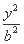=1的焦点在x轴上,过点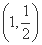作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆的方程是　　　　　　. 


    +=1


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


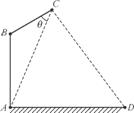
    在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与道路垂直,且∠ABC=120°,路灯C采用锥形灯罩,射出的光线如图中阴影部分所示,已知∠ACD=60°,路宽AD=24 m,设灯柱高AB=h(m),∠ACB=θ(30°≤θ≤45°).

    (1) 求灯柱的高h(用θ表示);

    (2) 若灯杆BC与灯柱AB所用材料相同,记此用料长度和为S,求S关于θ的函数解析式,并求出S的最小值.

    　(第11题)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正项数列{an}满足Sn=.

    (1) 求a1,a2,a3并推测an;

    (2) 用数学归纳法证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中,圆C的方程为ρ=4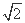cos,以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为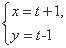(t为参数),求直线l被圆C截得的弦AB的长度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    抛物线x=y2的焦点坐标为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


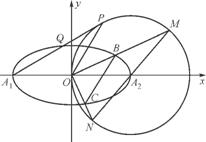
    如图,在平面直角坐标系xOy中,已知椭圆E: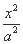+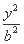=1(a>b>0)的离心率e=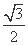,A1,A2分别是椭圆E的左、右两个顶点,圆A2的半径为a,过点A1作圆A2的切线,切点为P,在x轴的上方交椭圆E于点Q.

    (1) 求直线OP的方程;

    (2) 求的值;

    (3) 设a为常数,过点O作两条互相垂直的直线,分别交椭圆E于点B,C,分别交圆A2于点M,N,记OBC和OMN的面积分别为S1,S2,求S1·S2的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若随机变量X的概率分布为P(X=k)=,k=1,2,3,4,其中c是常数,则P<X<的值为　　　　.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列集合中表示同一集合的是(　　)

    A．M＝{(3,2)}，N＝{(2,3)}

    B．M＝{3,2}，N＝{2,3}

    C．M＝{(x，y)|x＋y＝1}，N＝{y|x＋y＝1}

    D．M＝{1,2}，N＝{(1,2)}

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在R上的函数f(x)，满足当x>0时，f(x)>1，且对任意的x，y∈R，有f(x＋y)＝f(x)·f(y)，f(1)＝2.

    (1)求f(0)的值；

    (2)求证：对任意x∈R，都有f(x)>0；

    (3)解不等式f(3－2x)>4.

    查看答案和解析>>

    同步练习册答案