
(12分)(12分)经过点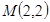 作直线
作直线 交双曲线
交双曲线 于
于 、
、 两点,且
两点,且 为
为 中点.
中点.
(1)求直线 的方程 ;(2)求线段
的方程 ;(2)求线段 的长.
的长.
(1)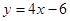 ; (2)
; (2)  。
。
解析试题分析:(1)在已知双曲线方程及弦中点的情况下可以采用点差法求直线的斜率,进而得到弦所在直线的方程.作差整后得一般表达式为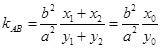 .
.
(2)求弦长问题要把直线方程与双曲线方程联立借助弦长公式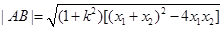 来求解.
来求解.
(1)设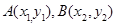 ,则
,则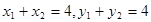 ,由
,由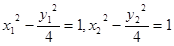 ,
,
得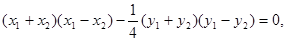 所以
所以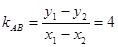 ,直线L的方程为
,直线L的方程为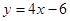 ---------5分
---------5分
经检验直线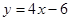 与双曲线有公共点,所以弦所在直线方程为
与双曲线有公共点,所以弦所在直线方程为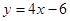 -----6分
-----6分
(2) 把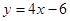 代入
代入 消去
消去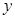 得
得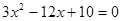
所以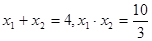 ,从而得
,从而得 ……… 12分
……… 12分
考点:直线与双曲线的位置关系,弦长,弦中点问题.
点评:(1)由双曲线或椭圆方程及弦中点的情况下可以采用点差法求直线的斜率,进而得到弦所在直线的方程.其作差后的一般形式为: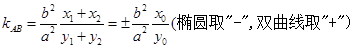 .
.
(2)求弦长时要用到弦长公式: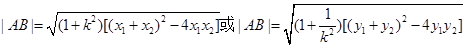 .
.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)过点(1,0)直线 交抛物线
交抛物线 于A(x1,y1),B(x2,y2)两点,抛物线的顶点是
于A(x1,y1),B(x2,y2)两点,抛物线的顶点是 .
.
(ⅰ)证明: 为定值;
为定值;
(ⅱ)若AB中点横坐标为2,求AB的长度及 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知焦点在 轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点
轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点 为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线 对称.
对称.
(1)求双曲线C的方程;
(2)设直线 与双曲线C的左支交于A,B两点,另一直线
与双曲线C的左支交于A,B两点,另一直线 经过M(-2,0)及AB的中点,求直线
经过M(-2,0)及AB的中点,求直线 在
在 轴上的截距b的取值范围.
轴上的截距b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
如图,已知椭圆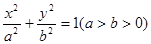 的长轴为
的长轴为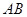 ,过点
,过点 的直线
的直线 与
与 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率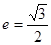

(1)求椭圆的标准方程;
(2)设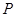 是椭圆上异于
是椭圆上异于 、
、 的任意一点,
的任意一点, 轴,
轴,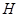 为垂足,延长
为垂足,延长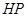 到点
到点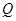 使得
使得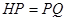 ,连接
,连接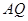 并延长交直线
并延长交直线 于点
于点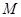 ,
,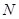 为
为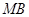 的中点.试判断直线
的中点.试判断直线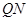 与以
与以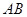 为直径的圆
为直径的圆 的位置关系.
的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com