（2014•天津二模）在实数集R中定义一种运算“⊕”，具有性质：
①对?a，b∈R，a⊕b=b⊕a；
②对?a∈R，a⊕0=a；
③对?a，b，c∈R，（a⊕b）⊕c=c⊕（ab）+（a⊕c）+（b⊕c）﹣2c；
那么函数f（x）=x⊕
（x≥1）的最小值为（ ）
A.5 B.4 C.2+2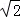
D.2
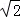
津桥教育计算小状元系列答案科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：填空题
（2014•陕西模拟）如图，EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，则∠A的大小为 ．
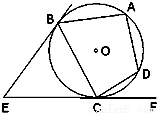
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷（解析版） 题型：选择题
如图，PA、PB是⊙O的切线，切点分别为A、B，点C在⊙O上．如果∠P=50°，那么∠ACB等于（ ）
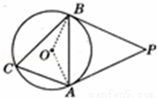
A.40° B.50° C.65° D.130°
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷（解析版） 题型：选择题
证明不等式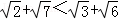
的最适合的方法是（ ）
A.综合法 B.分析法 C.间接证法 D.合情推理法
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.2数学证明练习卷（解析版） 题型：选择题
（2014•陕西模拟）已知[x]表示不超过实数x的最大整数（x∈R），如：[﹣1.3]=﹣2，[0.8]=0，[3.4]=3．定义{x}=x﹣[x]，求{
}+{
}+{
}+…+{
}=（ ）
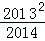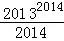A.1006 B.1007 C.1008 D.2014
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.2数学证明练习卷（解析版） 题型：选择题
（2014•潍坊三模）已知函数f（x）定义域为D，若?a，b，c∈D，f（a），f（b），f（c）都是某一三角形的三边，则称f（x）为定义在D上的“保三角形函数”，以下说法正确的个数有（ ）
①f（x）=1（x∈R）不是R上的“保三角形函数”
②若定义在R上的函数f（x）的值域为[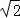
，2]，则f（x）一定是R上的“保三角形函数”
③f（x）=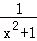
是其定义域上的“保三角形函数”
④当t＞1时，函数f（x）=ex+t一定是[0，1]上的“保三角形函数”
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.2数学证明练习卷（解析版） 题型：选择题
（2014•陕西一模）设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则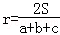
，类比这个结论可知：四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4，内切球半径为r，四面体S﹣ABC的体积为V，则r=（ ）
A.
B.
C.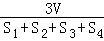
D.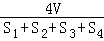
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 2.2结构图练习卷（解析版） 题型：选择题
把两条直线的位置关系填入结构图中的M、N、E、F中，顺序较为恰当的是（ ）
①平行 ②垂直 ③相交 ④斜交．
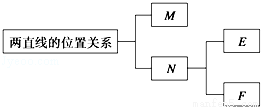
A.①②③④ B.①④②③ C.①③②④ D.②①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
）⊕0
﹣0≥2+2
，
如图梯形O′A′B′C′是一个平面图形的直观图，在直观图中，O′C′=C′B′=2O′A′=3，则原平面图形的面积为