
分析 根据函数奇偶性和单调性的关系将不等式进行转化求解即可.
解答 解:∵偶函数f(x)在[0,+∞)上单调递减,若f(2x-1)>f($\frac{5}{3}$)成立,
∴不等式等价为f(|2x-1|)>f($\frac{5}{3}$),
即|2x-1|<$\frac{5}{3}$,
即-$\frac{5}{3}$<2x-1<$\frac{5}{3}$,
得-$\frac{1}{3}$<x<$\frac{4}{3}$,
即x的取值范围是-$\frac{1}{3}$<x<$\frac{4}{3}$,
故答案为:-$\frac{1}{3}$<x<$\frac{4}{3}$.
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x2 | B. | $\frac{1}{3}$x2 | C. | -$\frac{2}{3}$x${\;}^{-\frac{1}{3}}$ | D. | $\frac{2}{3}$x${\;}^{-\frac{1}{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南石门县一中高三9月月考数学(文)试卷(解析版) 题型:填空题
在下列命题中所有正确命题的序号是 .
①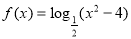 的单调减区间是
的单调减区间是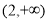 ;
;
②若函数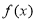 满足
满足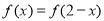 ,则
,则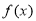 图象关于直线
图象关于直线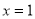 对称;
对称;
③函数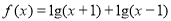 是偶函数;
是偶函数;
④设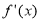 是函数
是函数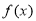 的导函数,若
的导函数,若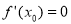 ,则
,则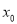 是
是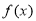 的极值点.
的极值点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com